题目内容
【题目】已知椭圆C:![]() 1(a>b>0)的一个顶点坐标为A(0,﹣1),离心率为
1(a>b>0)的一个顶点坐标为A(0,﹣1),离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=k(x﹣1)(k![]() 0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上.
0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(Ⅰ)由已知列出关于![]() 的方程组可解得结论;
的方程组可解得结论;
(Ⅱ)设P(x1,y1),Q(x2,y2),M(x0,y0),由直线方程与椭圆方程联立消去![]() 后整理,应用韦达定理得
后整理,应用韦达定理得![]() ,求出中点
,求出中点![]() 坐标,计算
坐标,计算![]() ,证明
,证明![]() 即可,
即可,
(Ⅰ)解:由题意可知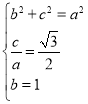
解得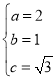
所以椭圆C的方程为![]() .
.
(Ⅱ)证明:设P(x1,y1),Q(x2,y2),M(x0,y0),.
由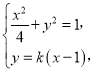 得(4k2+1)x2﹣8k2x+4k2﹣4=0,
得(4k2+1)x2﹣8k2x+4k2﹣4=0,
所以△=(﹣8k2)2﹣4×(4k2+1)(4k2﹣4)=48k2+16.
所以当k为任何实数时,都有△>0.
所以 ![]() ,
,![]() .
.
因为线段PQ的中点为M,
所以 ![]() ,
,![]() ,
,
因为 B(1,0),
所以 ![]() ,
,![]() .
.
所以 ![]()
![]()

 .
.
又因为 k![]() 0,
0,![]() ,
,
所以 ![]() ,
,
所以点M不在以AB为直径的圆上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目