题目内容
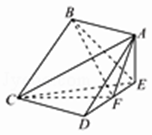
【题目】过正方体ABCD﹣A1B1C1D1的顶点A1在空间作直线l，使l与直线AC和BC1所成的角都等于 
，则这样的直线l共可以作出（ ）
A.1条
B.2条
C.3条
D.4条
【答案】C
【解析】解：因为AD1∥BC1，所以直线AC和BC1所成的角即为直线AC和AD1所成的角，所以过A1在空间作直线l，使l与直线AC和BC1所成的角都等于 
，即过点A在空间作直线l，使l与直线AC和AD1所成的角都等于 ．
因为∠ACD1=60°，∠ACD1的外角平分线与AC和AD1所成的角相等，均为60°，所以在平面ACD1内有一条满足要求．
因为∠ACD1的角平分线与AC和AD1所成的角相等，均为30°，将角平分线绕点A向上转动到与面ACD1垂直的过程中，存在两条直线与直线AC和BC1所成的角都等于 ，故符合条件的直线有3条．
故选C
【考点精析】关于本题考查的空间中直线与直线之间的位置关系，需要了解相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能得出正确答案．
练习册系列答案
名校课堂系列答案
相关题目
【题目】由于雾霾日趋严重，政府号召市民乘公交出行．但公交车的数量太多会造成资源的浪费，太少又难以满足乘客需求．为此，某市公交公司在某站台的60名候车乘客中进行随机抽样，共抽取10人进行调查反馈，所选乘客情况如下表所示：
组别 | 候车时间（单位：min） | 人数 |
一 | [0，5） | 1 |
二 | [5，10） | 5 |
三 | [10，15） | 3 |
四 | [15，20） | 1 |
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）现从这10人中随机取3人，求至少有一人来自第二组的概率；
（3）现从这10人中随机抽取3人进行问卷调查，设这3个人共来自X个组，求X的分布列及数学期望．
