题目内容
7.点集{(x,y)|||x|-1|+|y|=2}的图形是一条封闭的折线,这条封闭折线所围成的区域的面积是14.分析 根据方程特点,判断函数的对称性根据对称性求出方程在第一象限的面积即可得到结论.
解答 解:由于方程|||x|-1|+|y|=2 中,把x换成-x,方程不变,故方程表示的曲线关于y轴对称;
把y换成-y,方程也不变,故方程表示的曲线关于x轴及原点都对称,
即点集{(x,y)|||x|-1|+|y|=2}的图形关于x轴、y轴、及原点对称.
先考虑曲线位于第一象限及坐标轴上的情况.
令x≥0,y≥0,方程化为 y=2-|x|,表示线段AB 和BC,如图所示:

曲线在第一象限内围成的图形的面积等于直角梯形OABD的面积,加上直角三角形BDC的面积.
而直角梯形OABD的面积为$\frac{(1+2)×1}{2}$=$\frac{3}{2}$,直角三角形BDC的面积等于$\frac{1}{2}×2×2$=2,
故曲线在第一象限内围成的图形的面积等于$\frac{3}{2}$+2=$\frac{7}{2}$,
故整条封闭折线所围成的区域的面积是4×$\frac{7}{2}$=14,
故答案为:14
点评 本题主要考查带有绝对值的函数的图象特征,函数的对称性的应用,体现了分类讨论与数形结合的数学思想,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.展开(a+b+c)10合并同类项后的项数是( )
| A. | 11 | B. | 66 | C. | 76 | D. | 134 |
2.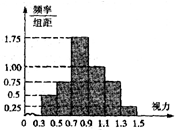 某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
 某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )
某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为( )| A. | 10 | B. | 20 | C. | 8 | D. | 16 |
12.已知函数f(x)=2ax3-3x2+1,若 f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
| A. | (1,+∞) | B. | (0,1) | C. | (-1,0) | D. | (-∞,-1) |
16.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则( )
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$方向相反 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$垂直 | D. | 以上都不对 |
17.过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | $\frac{7}{12}$ |
 如图,在△ABC中,AC=12,∠ABC=2∠C.
如图,在△ABC中,AC=12,∠ABC=2∠C.