题目内容
 四棱锥P-ABCD中,底面ABCD是边长为2a的正方形,各侧棱均与底面边长相等,E、F分别是PA、PC的中点.
四棱锥P-ABCD中,底面ABCD是边长为2a的正方形,各侧棱均与底面边长相等,E、F分别是PA、PC的中点.
(1)求证:PC∥平面BDE;
(2)求证:平面BDE丄平面BDF;
(3)求四面体E-BDF的体积.
解:(1)证明:连接AC交BD于O.连接OE.
在△PAC中,E、O分别是PA、AC的中点.
∴EO∥PC.
∵EO?平面BDE,PC?平面BDE,
∴PC∥平面BDE.
(2)证明:∵△PAB是等边三角形,且E是PA的中点,
∴BE⊥PA,同理DE⊥PA,
∴PA⊥平面BDE,
在△PAC中,F、O分别是PC、AC中点
∴OF⊥平面BDE,而OF?平面BDE,
∴平面BDE⊥平面BDF.
(3)解:∵OF⊥平面BDE,
∴VE-BDF=VF-BDE=
在等边三角形PAB中,PA=AB=2a,E是PA中点,
∴BE=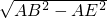 =
=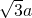 同理DE=
同理DE=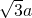 ,
,
∵BD=
在等腰三角形EBD中,EO是底边BD上的高
∴ ,显然,OF=EO,
,显然,OF=EO,
∴VE-BDF=VF-BDE=
= .
.
分析:(1)连接AC交BD于O.连接OE.E、O分别是PA、AC的中点.推出EO∥PC.然后证明PC∥平面BDE.
(2)证明BE⊥PA,DE⊥PA,推出PA⊥平面BDE,然后证明平面BDE⊥平面BDF.
(3)利用VE-BDF=VF-BDE= 求出BE、BD,然后求解体积.
求出BE、BD,然后求解体积.
点评:本题考查直线与平面平行,平面与平面垂直,几何体的体积的求法,考查空间想象能力,逻辑推理能力.
在△PAC中,E、O分别是PA、AC的中点.
∴EO∥PC.
∵EO?平面BDE,PC?平面BDE,
∴PC∥平面BDE.
(2)证明:∵△PAB是等边三角形,且E是PA的中点,
∴BE⊥PA,同理DE⊥PA,
∴PA⊥平面BDE,
在△PAC中,F、O分别是PC、AC中点
∴OF⊥平面BDE,而OF?平面BDE,
∴平面BDE⊥平面BDF.
(3)解:∵OF⊥平面BDE,
∴VE-BDF=VF-BDE=

在等边三角形PAB中,PA=AB=2a,E是PA中点,
∴BE=
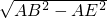 =
=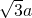 同理DE=
同理DE=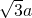 ,
,∵BD=

在等腰三角形EBD中,EO是底边BD上的高
∴
 ,显然,OF=EO,
,显然,OF=EO,∴VE-BDF=VF-BDE=

=
 .
.分析:(1)连接AC交BD于O.连接OE.E、O分别是PA、AC的中点.推出EO∥PC.然后证明PC∥平面BDE.
(2)证明BE⊥PA,DE⊥PA,推出PA⊥平面BDE,然后证明平面BDE⊥平面BDF.
(3)利用VE-BDF=VF-BDE=
 求出BE、BD,然后求解体积.
求出BE、BD,然后求解体积.点评:本题考查直线与平面平行,平面与平面垂直,几何体的体积的求法,考查空间想象能力,逻辑推理能力.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
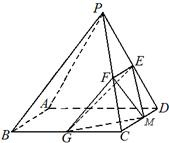 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.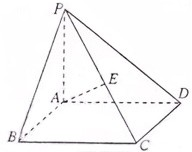 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2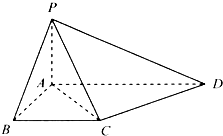 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=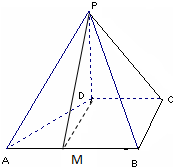 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.