题目内容
函数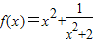
的最小值为（ ）A．0
B．
C．1
D．2
【答案】分析：令x2+2=t则t≥2，将函数转化成关于t的函数，然后利用导数研究函数y=t+
-2在[2，+∞）上的单调性，从而求出最值．
解答：解：令x2+2=t则t≥2
∴
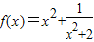转化成y=t-2+
=t+
-2其中t≥2
y′=1-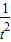
在[2，+∞）上恒大于0，则y=t+
-2在[2，+∞）上单调递增
∴y≥
故函数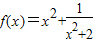
的最小值为
故选B．
点评：本题主要考查了函数的最值及其几何意义，以及利用导数研究函数的单调性，同时考查了换元法，属于中档题．
-2在[2，+∞）上的单调性，从而求出最值．解答：解：令x2+2=t则t≥2
∴
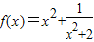转化成y=t-2+=t+-2其中t≥2y′=1-
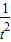在[2，+∞）上恒大于0，则y=t+-2在[2，+∞）上单调递增∴y≥
故函数
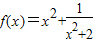的最小值为故选B．
点评：本题主要考查了函数的最值及其几何意义，以及利用导数研究函数的单调性，同时考查了换元法，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目