Question

【题目】如图，在四棱锥中，底面是边长为的正方形，，是的中点，是线段上异于端点的一点，平面 平面，.

（Ⅰ）证明：；

（Ⅱ）若与平面所成的角的正弦值为，求四棱锥的体积.

Answer 1

【答案】（1）见解析 （Ⅱ）

【解析】

（1）连接AC交BD与O，可证PA//平面BDM，再利用线面平行的性质定理和判定定理即可证得；

（2）根据已知条件建立空间直角坐标系，由线面所成角的正弦值为可得G的位置，即可求出梯形PAHG的面积，然后可以求四棱锥的体积.

解：（1）证明：连接AC交BD于点O，连接MO.

因为MO是△APC的中位线，所以MO//PA

又PA平面MBD，MO平面MBD，所以PA//平面MBD

又因为平面GAP∩平面BDM＝GH，PA平面GAP，所以PA//GH

又GH平面PAD，PA面PAD，所以GH//平面PAD

（2）如图建立空间直角坐标系.依题意可得D（0，0，0），A（2，0，0），C（0，2，0），P（0，0，2），M（0，1，1）

因为G在DM上，所以可设G（0，t，t），（0＜t＜1）

设是平面GAP的一个法向量，则

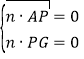即，

可取

若PD与平面GAP所成的角为α，

则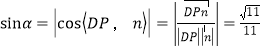

解得，则G是线段DM的中点

D到平面GAP的距离为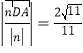

由（1）知MO//PA，PA//GH，所以MO//GH，所以H也是DO的中点，

经计算得

梯形PAHG的高为，面积为

四棱锥D-PAHG的体积