题目内容
(2012•珠海一模)有下列四种说法:
①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;
③“若am2<bm2,则a<b”的逆命题为真;
④若实数x,y∈[0,1],则满足:x2+y2<1的概率为
.
其中错误的个数是 ( )
①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;
③“若am2<bm2,则a<b”的逆命题为真;
④若实数x,y∈[0,1],则满足:x2+y2<1的概率为
| π |
| 4 |
其中错误的个数是 ( )
分析:求出特称命题的否定命题,可以判断①,根据复合命题真假判断的真值表和充要条件的定义,可判断②;写出原命题的逆命题,进而利用不等式的性质可以判断③;利用几何概型计算出概率,可以判断④
解答:解:对于①,根据含量词的命题的否定规则:量词交换结论否定得到①正确;
对于②,因为“命题p∨q为真”⇒命题p,q至少一个真;而“命题p∧q为真”⇒p,q全真,
所以②“命题p∨q为真”推不出“命题p∧q为真”反之,“命题p∧q为真”能推出“命题p∨q为真”,
所以“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;所以②正确;
对于③,“若am2<bm2,则a<b”的逆命题为“若a<b则am2<bm2”,当m=0时命题不成立,所以③错误;
对于④,实数x,y∈[0,1],构成的区域是变长为1的正方形其面积为1,
实数x,y∈[0,1]且满足:x2+y2<1构成的区域为半径为1的四分之一个圆,其面积为
,根据古典概型的概率公式得到概率为
.所以④正确.
故选B
对于②,因为“命题p∨q为真”⇒命题p,q至少一个真;而“命题p∧q为真”⇒p,q全真,
所以②“命题p∨q为真”推不出“命题p∧q为真”反之,“命题p∧q为真”能推出“命题p∨q为真”,
所以“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;所以②正确;
对于③,“若am2<bm2,则a<b”的逆命题为“若a<b则am2<bm2”,当m=0时命题不成立,所以③错误;
对于④,实数x,y∈[0,1],构成的区域是变长为1的正方形其面积为1,
实数x,y∈[0,1]且满足:x2+y2<1构成的区域为半径为1的四分之一个圆,其面积为
| π |
| 4 |
| π |
| 4 |
故选B
点评:本题以命题的真假判断为载体,考查了特称命题的否定,四种命题,充要条件,几何概型,不等式的性质,是简单逻辑的综合应用,但难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
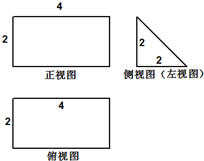 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知