题目内容
3.抛物线y2=2px(p>0)的焦点为F,A、B为抛物线上的两个动点,且满足∠AFB=60°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则$\frac{|MN|}{|AB|}$的最大值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | 2 |
分析 设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2-3ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.
解答  解:设|AF|=a,|BF|=b,
解:设|AF|=a,|BF|=b,
由抛物线定义,得AF|=|AQ|,|BF|=|BP|
在梯形ABPQ中,∴2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2-2abcos60°=a2+b2-ab
配方得,|AB|2=(a+b)2-3ab,
又∵ab≤($\frac{a+b}{2}$) 2,
∴(a+b)2-3ab≥(a+b)2-$\frac{3}{4}$(a+b)2=$\frac{1}{4}$(a+b)2
得到|AB|≥$\frac{1}{2}$(a+b).
∴$\frac{|MN|}{|AB|}$≤1,即$\frac{|MN|}{|AB|}$的最大值为1.
故选C.
点评 本题着重考查抛物线的定义和简单几何性质、基本不等式求最值和余弦定理的应用等知识,属于中档题.

练习册系列答案
相关题目
18.若a、b、c∈R,且ab+bc+ca=1,则下列不等式成立的是( )
| A. | a2+b2+c2≥2 | B. | (a+b+c)2≥3 | C. | $\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥2$\sqrt{3}$ | D. | a+b+c≤$\sqrt{3}$ |
14.如图是函数y=f (x)的部分图象,下列数值排序正确的是( )
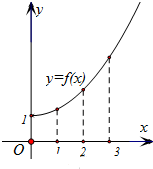

| A. | f (3)<f′(2)+f (2) | B. | f (3)>f′(3)+f (2) | C. | f (2)>f′(2)+f (1) | D. | f (2)>f′(1)+f (1) |
11.已知抛物线C:y2=2px(p>0),焦点为F,准线为l,P为抛物线上一点,过点P作直线l的垂线PM,垂足为M,已知△PFM为等边三角形,则△PFM的面积为( )
| A. | p2 | B. | $\sqrt{3}$p2 | C. | 2p2 | D. | 2$\sqrt{3}$p2 |
15.已知抛物线y=x2-1上的一定点B(-1,0)和两个动点P、Q,当BP⊥PQ时,点Q的横坐标的取值范围是( )
| A. | (-∞,-3]∪[1,+∞) | B. | [-3,1] | ||
| C. | (-∞,-3]∪[1,$\frac{3}{2}$)∪($\frac{3}{2}$,+∞) | D. | [1,+∞) |