题目内容
4．在Rt△ABC中，若∠C=90°，则cos2A+cos2B=1，请在立体几何中给出类似的四面体性质的猜想．分析 由勾股定理是平面二维的关系，类比到三维空间可猜测“在三棱锥P-ABC中，三个侧面PAB、PAC、PCB两两垂直，且与底面所成的角分别为α，β，γ，则cos2α+cos2β+cos2γ=1”．
解答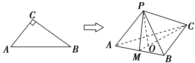 
解：如图，由平面类比到空间，有下列猜想：
“在三棱锥P-ABC中，三个侧面PAB、PAC、PCB两两垂直，且与底面所成的角分别为α，β，γ，则cos2α+cos2β+cos2γ=1”．
点评 本题考查类比的方法猜想三棱锥的类似性质，体现了数形结合的数学思想，解题时要注意空间思维能力的培养．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
14．抛物线y2=4x的焦点坐标为（ ）
| A． | （2，0） | B． | （0，2） | C． | （1，0） | D． | （0，1） |
12．若直线y=3x上存在点（x，y）满足约束条件 $\left\{\begin{array}{l}{x+y+4≥0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$，则实数m的取值范围是（ ）
| A． | [-1，+∞） | B． | （-1，+∞） | C． | （-∞，-1] | D． | （-∞，-1） |
根据最新修订的《环境空气质量标准》指出空气质量指数在0：50，各类人群可正常活动．某市环保局在2014年对该市进行了为期一年的空气质量检测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为[0，10），[10，20），[20，30），[30，40），[40，50]，由此得到样本的空气质量指数频率分布直方图，如图．