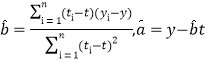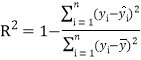题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,判断并证明函数
时,判断并证明函数![]() 在
在![]() 上单调性。
上单调性。
(2)当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围。
的取值范围。
【答案】(1)单调递增(2)![]()
【解析】试题分析:(1)设![]() ,比较
,比较![]() 和0的大小,从而得
和0的大小,从而得![]() 在
在![]() 上的单调性
上的单调性
(2)首先![]() 时可证明函数
时可证明函数![]() 为奇函数,且在
为奇函数,且在![]() 上单调递增,从而转化为
上单调递增,从而转化为![]() 在
在![]() 上有解,进而转化为函数
上有解,进而转化为函数![]() 与函数
与函数![]() 有交点,所以
有交点,所以![]() ,即
,即![]()
试题解析:(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,证明如下:
上单调递增,证明如下:
设![]() ,则
,则
![]()
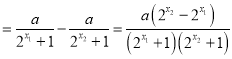
因为![]() ,所以
,所以![]() ,
, ![]() ,又
,又![]()
所以![]() 即
即![]()
所以,函数![]() 在
在![]() 上单调递增
上单调递增
(2)当![]() 时,
时, ![]() ,定义域为
,定义域为![]()
![]()
所以,函数![]() 为奇函数
为奇函数
因为![]()
所以![]()
由(1)知, ![]() 时,函数
时,函数![]() 在
在![]() 上单调递增
上单调递增
所以![]() 在
在![]() 上有解,
上有解,
所以函数![]() 与函数
与函数![]() 有交点
有交点
所以![]() ,即
,即![]()
所以实数![]() 的取值范围为
的取值范围为![]()
点晴:证明函数单调性的一般步骤:(1)取值:在定义域上任取![]() ,并且
,并且![]() (或
(或![]() );(2)作差:
);(2)作差: ![]() ,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断
,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断![]() 的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.
的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.

 名校课堂系列答案
名校课堂系列答案【题目】沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的![]() 、
、![]() 两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
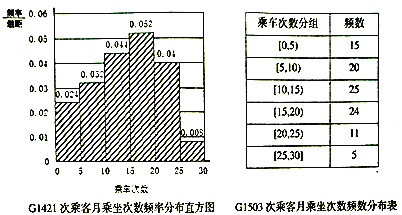
(1)若将频率视为概率,月乘车次数不低于15次的称之为“老乘客”,试问:哪一车次的“老乘客”较多,简要说明理由;
(2)已知在![]() 次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成
次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成![]() 列联表,并根据资料判断,是否有
列联表,并根据资料判断,是否有![]() 的把握认为年龄与乘车次数有关,说明理由.
的把握认为年龄与乘车次数有关,说明理由.
老乘客 | 新乘客 | 合计 | |||||||
50岁以上 | |||||||||
50岁以下 | |||||||||
合计 | |||||||||
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | ||||
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | ||||
附:随机变量 (其中
(其中![]() 为样本容量)
为样本容量)
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
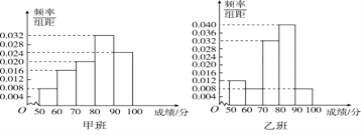
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |