题目内容
解答题
已知椭圆的中心在原点，焦点在x轴上，一个顶点坐标为A(0，－1)，且其右焦点到直线x－y＋2
＝0的距离为3．
(1)求椭圆的方程；
(2)是否存在斜率为k的直线l，使l与已知曲线交于不同两点M、N，且有|AM|＝|AN|，若存在，求k的范围；若不存在，说明理由．
答案：
解析：
解析：
|
(1)依题意可设椭圆方程为 ∴右焦点坐标为( 由点到直线距离公式得3＝ ∴椭圆方程为 (2)设这样的直线存在，设l方程为y＝kx＋m，代入椭圆方程(1＋3k2)x2＋6kmx＋3(m2－1)＝0． ∵直线l与椭圆交于M、N两点， ∴Δ＞0，即36k2m2－12(1＋3k2)(m2－1)＞0． 化简得m2＜3k2＋1． (*) 而|AM|＝|AN|可等价转化为直线l的垂直平分线过点A， 设M(x1，y1)，N(x2，y2)，弦MN中点(x0，y0)． 由韦达定理x1＋x2＝ ∴x0＝ ∴y0＝ ∴－ 化简得m＝ 解得－1＜k＜1，故存在直线l使|AM|＝|AN|． |
＋
＝1，
，0)．
，解得a2＝3．
＋y2＝1．
，
，
．
＝
，
，代入(*)式得(
)2＜3k2＋1，
练习册系列答案
相关题目
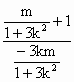选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
＋
＝1(________)的两个焦点，P是椭圆上一点，且∠F1PF2＝
，则△F1PF2的面积是b2．请将题目中空缺的一个可能条件填入“________”处．
(0，－
)，对应准线是y＝－
，并且
和
的等比中项是离心率e．
平分，试求直线l的倾斜角的取值范围．
＋
＝1的焦点为F1、F2，能否在x轴下方的椭圆弧上找到一点M，使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项？若存在，求出M点坐标；若不存在，说明理由．
＝0的距离为3．
若存在，求出m的值；若不存在，请说明理由．