题目内容
解答题
已知椭圆
＋
＝1的焦点为F1、F2，能否在x轴下方的椭圆弧上找到一点M，使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项？若存在，求出M点坐标；若不存在，说明理由．
答案：
解析：
解析：
|
由方程得a＝2，b＝ ∴e＝ 设满足条件的点M(x0，y0)(－2≤y0＜0)，则有 |MN|2＝|MF1|·|MF2|． 由焦半径公式有(y0＋4)2＝(2＋ |
，c＝1，
，∴下准线方程为y＝－4．
y0)(2－
y0)，解得y0＝－
或－4．与y0≥－2矛盾．故不存在这样的点M．
练习册系列答案
相关题目
＋
＝1上一点P，到其左、右两焦点距离之比为1∶3，求点P到两准线的距离及点P的坐标．
＋
＝1的焦点为F1和F2，抛物线与椭圆在第一象限内的交点为Q，且∠F1QF2＝
，求抛物线的方程．
(0，－1)和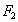
(0，1)，直线y＝4是该椭圆的一条准线．
＝1，求tan∠
＋
＝1(a＞b＞0)上有两点A、B，直线y＝x＋m上有两点C、D，且ABCD是正方形，正方形的外接圆的方程为x2＋y2－2y－8＝0，求椭圆和直线的方程．