题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:依题意,设椭圆的方程为
∴椭圆方程为 |
(2) |
解:设M(x1,y1),N(x2,y2),由
∴ 但此时判别式 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| |||||||||||
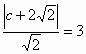 -----------4分
-----------4分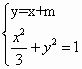 得4x2+6mx+3m2-3=0当判别式△>0时
得4x2+6mx+3m2-3=0当判别式△>0时