题目内容
11．已知f（x）的导函数为f′（x）且满足f（x）=x3+f′（$\frac{2}{3}$）x2-x，则f（$\frac{2}{3}$）=-$\frac{22}{27}$．分析 对函数f（x）的解析式求导，得到其导函数，把x=$\frac{2}{3}$代入导函数中，列出关于f′（$\frac{2}{3}$）的方程，进而得到f′（$\frac{2}{3}$）的值，确定出函数f（x）的解析式，把x=$\frac{2}{3}$代入
f（x）解析式，即可求出f（$\frac{2}{3}$）的值．
解答 解：由f（x）=x3+f′（$\frac{2}{3}$）x2-x，得f′（x）=3x2+2f′（$\frac{2}{3}$）x-1，
∴$f′（\frac{2}{3}）=3×（\frac{2}{3}）^{2}+2×\frac{2}{3}f′（\frac{2}{3}）-1$，解得：f′（$\frac{2}{3}$）=-1．
∴f（x）=x3-x2-x，
则f（$\frac{2}{3}$）=$（\frac{2}{3}）^{3}-（\frac{2}{3}）^{2}-\frac{2}{3}$=-$\frac{22}{27}$．
故答案为：-$\frac{22}{27}$．
点评 此题考查了导数的运算，以及函数的值．运用求导法则得出函数的导函数，求出常数f′（$\frac{2}{3}$）的值，从而确定出函数的解析式是解本题的关键，是中档题．
练习册系列答案
相关题目
1．
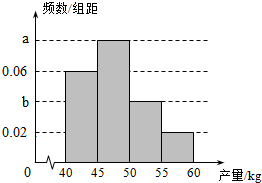果农种了一片果树，收获时，果农随机随机选取果树20株作为样本．测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的$\frac{4}{3}$倍．
（1）求a，b的值；
（2）果树的价格如下表：
若果农从这20株样本中随机抽取两株以总价400元卖出，求果农获利的分布和期望．
果农种了一片果树，收获时，果农随机随机选取果树20株作为样本．测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的$\frac{4}{3}$倍．（1）求a，b的值；
（2）果树的价格如下表：
| 产量 | （40，45] | （45，50] | （50，55] | （55，60] |
| 价格（百元/棵） | 1 | 2 | 3 | 4 |
1．已知函数f（x）的定义域为（0，+∞），若y=$\frac{f（x）}{x}$在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=$\frac{f（x）}{{x}^{2}}$在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．我们把所有“一阶比增函数”组成的集合记为Ω1，所有“二阶比增函数”组成的集合记为Ω2，．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
求证：d（2d+t-4）＞0；
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
| x | a | b | c | a+b+c |
| f（x） | d | d | t | 4 |
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．