题目内容
从集合{x|-5≤x≤16,x∈Z}中任选2个数,作为方程
+
=1中的m和n,
求:(1)可以组成多少个双曲线?
(2)可以组成多少个焦点在x轴上的椭圆?
(3)可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆?
| x2 |
| m |
| y2 |
| n |
求:(1)可以组成多少个双曲线?
(2)可以组成多少个焦点在x轴上的椭圆?
(3)可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆?
集合中共有16个正数,5个负数
(1)若能构成双曲线,则mn<0
因此,共有5×16×2=160个…(5分)
(2)若能构成焦点在x轴上的椭圆,则m>n>0
因此,共有
=120个…(5分)
(3)因为|x|≤2,|y|≤3,∴m≤4,n≤9,
因此,共有4×8=32个…(5分)
(1)若能构成双曲线,则mn<0
因此,共有5×16×2=160个…(5分)
(2)若能构成焦点在x轴上的椭圆,则m>n>0
因此,共有
| 16×15 |
| 2 |
(3)因为|x|≤2,|y|≤3,∴m≤4,n≤9,
因此,共有4×8=32个…(5分)

练习册系列答案
相关题目
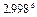 的近似值(精确到小数后第三位)为
的近似值(精确到小数后第三位)为