题目内容
(本小题8分)已知圆C: 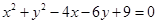 及直
及直
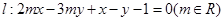
(1)证明:不论m取何值,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长最短时的直线方程.
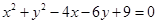 及直
及直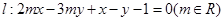
(1)证明:不论m取何值,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长最短时的直线方程.
(1)见解析;(2)y=x-1。
本题考查直线与圆相交的证明,考查直线被圆截得的线段的最短长度以及此时直线的方程.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
解:由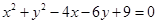 得
得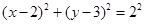
∴圆C的圆心为(2,3),半径为2……………2分
(1)由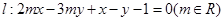 得
得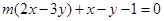
由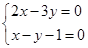 得
得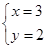
∴不论m取何值,直线l恒过点P(3,2)…………….4分
∵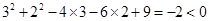
∴点P(3,2)在圆C内……………3分
所以不论m取何值,直线l与圆C恒相交…………….5分
(2)当直线l垂直CP时,直线l被圆C截得的弦长最短
∵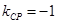 …………….7分
…………….7分
所以所求的直线方程为y=x-1…………….8分
解:由
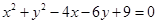 得
得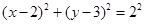
∴圆C的圆心为(2,3),半径为2……………2分
(1)由
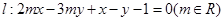 得
得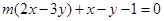
由
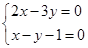 得
得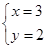
∴不论m取何值,直线l恒过点P(3,2)…………….4分
∵
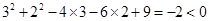
∴点P(3,2)在圆C内……………3分
所以不论m取何值,直线l与圆C恒相交…………….5分
(2)当直线l垂直CP时,直线l被圆C截得的弦长最短
∵
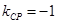 …………….7分
…………….7分所以所求的直线方程为y=x-1…………….8分

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
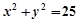 ,
,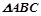 内接于此圆,
内接于此圆,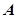 点的坐标
点的坐标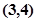 ,
,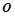 为坐标原点.
为坐标原点.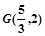 ,求直线
,求直线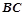 的方程;
的方程;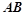 与直线
与直线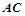 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线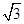 ),且斜率为1,求l与C相交所得的弦长.
),且斜率为1,求l与C相交所得的弦长.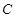 :
: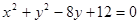 ,和定点
,和定点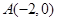 ,
,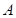 作圆
作圆 ,求直线
,求直线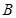 两点,且
两点,且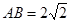 时,求直线
时,求直线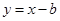 与曲线
与曲线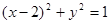 有两个不同的公共点,则实数
有两个不同的公共点,则实数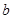 的取值范围为( )
的取值范围为( )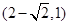
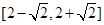
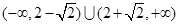
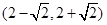
 中,已知圆
中,已知圆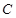 经过点
经过点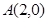 和点
和点 ,且圆心
,且圆心 上,过点
上,过点 且斜率为
且斜率为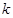 的直线与圆
的直线与圆 .
.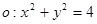 和点
和点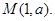
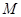 有且只有一条直线与圆
有且只有一条直线与圆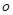 相切,求实数
相切,求实数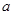 的值,并求出切线方程;
的值,并求出切线方程;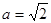 ,过点
,过点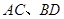 ,且
,且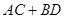 的最大值。
的最大值。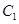 :
: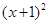 +
+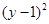 =1,圆
=1,圆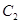 与圆
与圆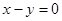 对称,则圆
对称,则圆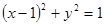
 相切,且与圆
相切,且与圆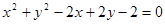 外切的面积最小的圆的方程为 .
外切的面积最小的圆的方程为 .