题目内容
某种商品,原来定价每件p元,每月能卖出n件,假若定价上涨x成(这里x成即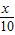 ,且0<x≤10),每月卖出数量将减少y成,而售货金额变成原来的z倍.
,且0<x≤10),每月卖出数量将减少y成,而售货金额变成原来的z倍.(1)设y=
 x,求售货金额最大时的x值;
x,求售货金额最大时的x值;(2)若y=
 x,求使售货金额比原来有所增加的x值的范围.
x,求使售货金额比原来有所增加的x值的范围.
【答案】分析:(1)根据售货金额=单件定价×销售量建立函数关系,然后基本不等式求出函数的最值;
(2)要使售货金额比原来有所增加,当且仅当z>1时才满足要求,建立不等式关系,解之即可求出所求.
解答:解:(1)由题意知,某商品定价若上涨x成,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+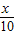 )元、n(1-
)元、n(1- )件、znp元.
)件、znp元.
∴znp=p(1+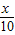 )n(1-
)n(1-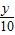 ),
),
又y= x,
x,
∴z= (1+
(1+ )(2-
)(2- ).
).
由已知1+ >0,2-
>0,2-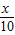 >0,
>0,
∴z≤ 2=
2= ,
,
当且仅当1+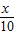 =2-
=2- ,
,
即x=5时,取“=”号,得x=5∈(0,10].
∴售货金额最大时x的值为5.
(2)当y= x时,
x时,
z=(1+ )(1-
)(1- )=
)=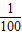 (10+x)(10-
(10+x)(10- x).
x).
显然,要使售货金额比原来有所增加,
当且仅当z>1时才满足要求.
由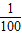 (10+x)(10-
(10+x)(10- x)>1,得0<x<5.
x)>1,得0<x<5.
∴使售货金额比原来有所增加的x值的范围是(0,5).
点评:本题主要考查了基本不等式在最值问题中的应用,同时考查了运算求解的能力,属于中档题.
(2)要使售货金额比原来有所增加,当且仅当z>1时才满足要求,建立不等式关系,解之即可求出所求.
解答:解:(1)由题意知,某商品定价若上涨x成,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+
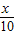 )元、n(1-
)元、n(1- )件、znp元.
)件、znp元.∴znp=p(1+
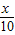 )n(1-
)n(1-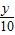 ),
),又y=
 x,
x,∴z=
 (1+
(1+ )(2-
)(2- ).
).由已知1+
 >0,2-
>0,2-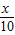 >0,
>0,∴z≤
 2=
2= ,
,当且仅当1+
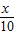 =2-
=2- ,
,即x=5时,取“=”号,得x=5∈(0,10].
∴售货金额最大时x的值为5.
(2)当y=
 x时,
x时,z=(1+
 )(1-
)(1- )=
)=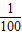 (10+x)(10-
(10+x)(10- x).
x).显然,要使售货金额比原来有所增加,
当且仅当z>1时才满足要求.
由
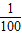 (10+x)(10-
(10+x)(10- x)>1,得0<x<5.
x)>1,得0<x<5.∴使售货金额比原来有所增加的x值的范围是(0,5).
点评:本题主要考查了基本不等式在最值问题中的应用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
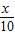 ,且0<x≤10),每月卖出数量将减少y成,而售货金额变成原来的z倍.
,且0<x≤10),每月卖出数量将减少y成,而售货金额变成原来的z倍. x,求售货金额最大时的x值;
x,求售货金额最大时的x值; x,求使售货金额比原来有所增加的x值的范围.
x,求使售货金额比原来有所增加的x值的范围.