题目内容
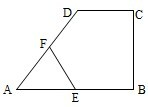 如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=
如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=| a | 2 |
分析:要求EF的长,关键是关键是构造一个三角形,使EF位于该三角形,解三角形即可求解:
解答:解:连接DE,
∵四边形ABCD为直角梯形,AB=AD=a,CD=
,CB⊥AB,点E,F分别为线段AB,AD的中点
∴△AED为直角三角形.则EF是RT△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=
DE=
AB=
.
故答案为:
∵四边形ABCD为直角梯形,AB=AD=a,CD=
| a |
| 2 |
∴△AED为直角三角形.则EF是RT△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
故答案为:
| a |
| 2 |
点评:连接DE,构造含有线段EF的直角三角形是解答本题的关键,由此可得,解决平面几何的求值和证明问题,辅助线的添加是基础.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则