题目内容
用反证法证明命题:“已知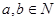 ,若
,若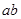 可被5整除,则
可被5整除,则 中至少有一个能被5整除”时,反设正确的是( )
中至少有一个能被5整除”时,反设正确的是( )
A. 都不能被5整除 都不能被5整除 | B. 都能被5整除 都能被5整除 |
C. 中有一个不能被5整除 中有一个不能被5整除 | D. 中有一个能被5整除 中有一个能被5整除 |
A
解析试题分析:根据肯定题设而否定结论,用反证法证明命题:“已知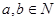 ,若
,若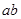 可被5整除,则
可被5整除,则 中至少有一个能被5整除”时,反设正确的是“
中至少有一个能被5整除”时,反设正确的是“ 都不能被5整除”,选A。
都不能被5整除”,选A。
考点:反证法
点评:简单题,反证法是“间接证明法”一类,是从反方向证明的证明方法,即:肯定题设而否定结论,从而得出矛盾。在应用反证法证题时,一定要用到“反设”,否则就不是反证法。

练习册系列答案
相关题目
用数学归纳法证明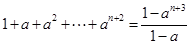 (
(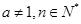 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为
| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
用数学归纳法证明不等式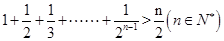 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )
A.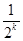 | B.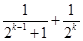 |
C.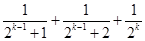 | D. |
观察下列各式: =3125,
=3125, =15625,
=15625, =78125, ,则
=78125, ,则 的末四位数字为( )
的末四位数字为( )
| A.3125 | B.5625 | C.0625 | D.8125 |
用反证法证明命题“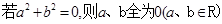 ”,其反设正确的是( )
”,其反设正确的是( )
A.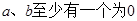 | B.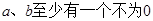 |
C.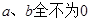 | D. |
有一段演绎推理是这样的,“有些有理数是分数,整数是有理数,则整数是分数”,结论显然是错误的,因为
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
设n是自然数,则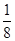 (n2-1)[1-(-1)n]的值 ( )
(n2-1)[1-(-1)n]的值 ( )
| A.一定是零 | B.不一定是整数 |
| C.一定是偶数 | D.是整数但不一定是偶数 |
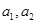 是正实数,则有
是正实数,则有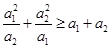 ”推广到一般情形,推广后的命题为____________.
”推广到一般情形,推广后的命题为____________. 中,得出的一般性结论是__________.
中,得出的一般性结论是__________.