题目内容
已知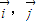 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设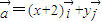 ,
,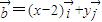 ,且满足
,且满足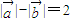
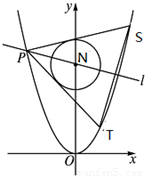
(1)求点P(x,y)的轨迹E的方程.
(2)若直线l过点F2(2,0)且法向量为
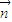 =(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,
=(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,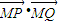 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围.
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围.
【答案】分析:(1)条件“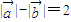 ”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;
”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;
(2)设直线l的方程为y=-t(x-2),将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得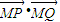 值,从而解决问题.
值,从而解决问题.
解答:解:(1)由条件“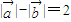 ”知:动点到两定点的距离之差为2,是双曲线,
”知:动点到两定点的距离之差为2,是双曲线,
故方程为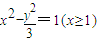 ,((4分)+(1分)定义域)
,((4分)+(1分)定义域)
(2)设直线l的方程为t(x-2)+y=0或y=-t(x-2)(1分)
由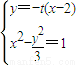 得(t2-3)x2-4t2x+4t2+3=0(1分)
得(t2-3)x2-4t2x+4t2+3=0(1分)
设P(x1,y1),Q(x2,y2)
由条件得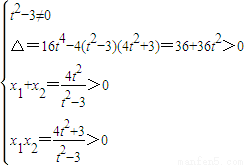 (只计算△=36+36t2>01分)
(只计算△=36+36t2>01分)
解得t2>3即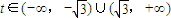 ((1分)
((1分)
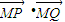 =(x1+1)(x2+1)+y1y2(1分)
=(x1+1)(x2+1)+y1y2(1分)
=x1x2+x1+x2+1+t2(x1-2)(x2-2)(1分)
=(t2+1)x1x2-(2t2-1)(x1+x2)+1+4t2(1分)
=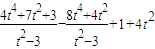 =0(2分).
=0(2分).
点评:(1)平面向量与解析几何的结合通常涉及轨迹等问题的处理,目标是将几何问题坐标化、符号化、数量化,从而将推理转化为运算,或者考虑向量运算的几何意义,利用其几何意义解决有关问题;(2)直线l与点P的轨迹的交点问题,组成方程组解决.
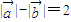 ”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;
”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;(2)设直线l的方程为y=-t(x-2),将直线的方程代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得
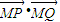 值,从而解决问题.
值,从而解决问题.解答:解:(1)由条件“
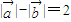 ”知:动点到两定点的距离之差为2,是双曲线,
”知:动点到两定点的距离之差为2,是双曲线,故方程为
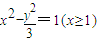 ,((4分)+(1分)定义域)
,((4分)+(1分)定义域)(2)设直线l的方程为t(x-2)+y=0或y=-t(x-2)(1分)
由
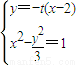 得(t2-3)x2-4t2x+4t2+3=0(1分)
得(t2-3)x2-4t2x+4t2+3=0(1分)设P(x1,y1),Q(x2,y2)
由条件得
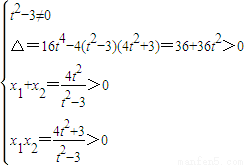 (只计算△=36+36t2>01分)
(只计算△=36+36t2>01分)解得t2>3即
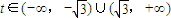 ((1分)
((1分)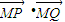 =(x1+1)(x2+1)+y1y2(1分)
=(x1+1)(x2+1)+y1y2(1分)=x1x2+x1+x2+1+t2(x1-2)(x2-2)(1分)
=(t2+1)x1x2-(2t2-1)(x1+x2)+1+4t2(1分)
=
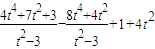 =0(2分).
=0(2分).点评:(1)平面向量与解析几何的结合通常涉及轨迹等问题的处理,目标是将几何问题坐标化、符号化、数量化,从而将推理转化为运算,或者考虑向量运算的几何意义,利用其几何意义解决有关问题;(2)直线l与点P的轨迹的交点问题,组成方程组解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点, ),求直线l的斜率k的取值范围.
),求直线l的斜率k的取值范围.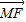 =λ
=λ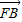 (λ>0)
(λ>0)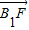 |,|
|,|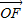 |,2|
|,2|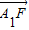 |成等差数列求λ的值
|成等差数列求λ的值