��Ŀ����
��֪�����ߵĶ���������ԭ��O������F��x���������ϣ���б��Ϊ��ǵ�ֱ��l��F�㣬��ֱ��l�������߽���A��B���㣬�������ߵ��߽���M�㣬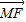 =��
=��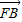 ���ˣ�0��
���ˣ�0����1������=1����ֱ��lб��
��2������A��B��x���ϵ���Ӱ�ֱ�ΪA1��B1��|
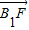 |��|
|��|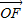 |��2|
|��2|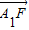 |�ɵȲ�������˵�ֵ
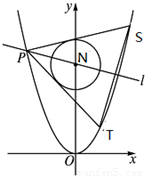
|�ɵȲ�������˵�ֵ��3������֪������ΪC1��y2=x�������ƶ��㰴��ʱ�뷽����ת90°���C1����ԲC2��x2+��y-4��=1��Բ��Ϊ��N����֪��P��������C1����һ�㣨����ԭ�㣩������P��ԲC2���������ߣ���������C��1��T��S�����㣬����N��P�����ֱ��l��ֱ��TS����ֱ��l�ķ��̣�
���𰸡���������1����ȷ��p=�ˣ�x2-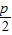 �����������B�����꣬������ֱ��l��б�ʣ�
�����������B�����꣬������ֱ��l��б�ʣ�
��2��ֱ�߷��̴��������߷��̣����A1��B1�ĺ����꣬����|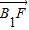 |��|
|��|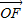 |��2|
|��2|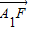 |�ɵȲ����У��ɵ�2|
|�ɵȲ����У��ɵ�2|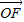 |=|
|=|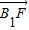 |+2|
|+2|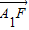 |���Ӷ��ɵ�x2-2x1=
|���Ӷ��ɵ�x2-2x1=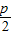 ���ɴ˿���˵�ֵ��
���ɴ˿���˵�ֵ��
��3�������P��ԲC2�����߷��̣��ɵ�PS��PT��б���Ƿ��̵�����������Τ�ﶨ���������������������ɵõ����ۣ�
����⣺�������������߷���Ϊy2=2px��p��0����A��x1��y1����B��x2��y2����ֱ��l��б��Ϊk��k��0��M��������Ϊy��
��F��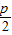 ��0���߷���Ϊx=-
��0���߷���Ϊx=-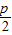
ֱ��l�ķ���Ϊy=k��x-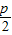 ����M��-
����M��-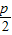 ��y����y2��0
��y����y2��0
��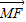 =��
=��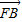 ���ࣨp��-y��=�ˣ�x2-
���ࣨp��-y��=�ˣ�x2-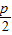 ��y������p=�ˣ�x2-
��y������p=�ˣ�x2-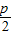 ��
��
��1������=1����p=�ˣ�x2-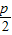 ����y22=2px2��y2��0����x2=
����y22=2px2��y2��0����x2=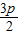 ��y2=
��y2=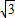 p��
p��
��B��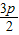 ��
��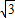 p��
p��
��ֱ��l��б��k=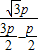 =
=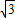 ��
��
��2��ֱ��l�ķ��̴���y2=2px����ȥy���ɵ�k2x2-��k2p+2p��x+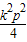 =0����x1x2=
=0����x1x2=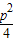
��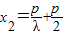 ����
����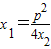 =
=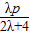
��|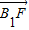 |��|
|��|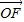 |��2|
|��2|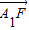 |�ɵȲ�����
|�ɵȲ�����
��2|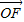 |=|
|=|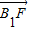 |+2|
|+2|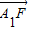 |��
|��
��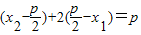
��x2-2x1=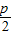
��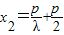 ��
��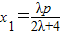 ������ʽ��
������ʽ��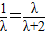 �����=2��
�����=2��
��3����P��x��x2����S��x1��x12����T��x2��x22�����������x��0��x��±1��x1��x2��
�����P��ԲC2�����߷���Ϊy-x2=k��x-x������y=kx-kx+x2����
��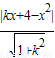 =1��
=1��
����x2-1��k2+2x��4-x2��k+��x2-4��2-1=0��
��PS��PT��б��Ϊk1��k2��k1��k2������k1��k2���������̵�����������
k1+k2=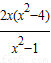 ��k1k2=
��k1k2=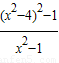 ��
��
���ٴ���y=x2����x2-kx+kx-x2=0��
����x�Ǵ˷��̵ĸ�����x1=k1-x��x2=k2-x��
����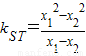 =x1+x2=k1+k2-2x=
=x1+x2=k1+k2-2x=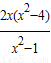 -2x��kNP=
-2x��kNP=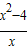 ��
��
��MP��AB����kNP•kST=[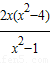 -2x]•
-2x]•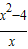 =-1�����x2=
=-1�����x2=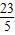 ��
��
����P��������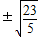 ��
��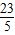 ��������ֱ��l�ķ���Ϊ
��������ֱ��l�ķ���Ϊ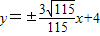 ��
��
���������⿼��ֱ���������ߵ�λ�ù�ϵ������Ȳ����е����ʣ�����ѧ�������������������������е��⣮
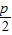 �����������B�����꣬������ֱ��l��б�ʣ�
�����������B�����꣬������ֱ��l��б�ʣ���2��ֱ�߷��̴��������߷��̣����A1��B1�ĺ����꣬����|
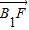 |��|
|��|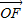 |��2|
|��2|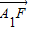 |�ɵȲ����У��ɵ�2|
|�ɵȲ����У��ɵ�2|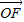 |=|
|=|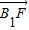 |+2|
|+2|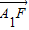 |���Ӷ��ɵ�x2-2x1=
|���Ӷ��ɵ�x2-2x1=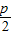 ���ɴ˿���˵�ֵ��
���ɴ˿���˵�ֵ����3�������P��ԲC2�����߷��̣��ɵ�PS��PT��б���Ƿ��̵�����������Τ�ﶨ���������������������ɵõ����ۣ�
����⣺�������������߷���Ϊy2=2px��p��0����A��x1��y1����B��x2��y2����ֱ��l��б��Ϊk��k��0��M��������Ϊy��
��F��
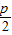 ��0���߷���Ϊx=-
��0���߷���Ϊx=-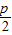
ֱ��l�ķ���Ϊy=k��x-
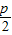 ����M��-
����M��-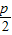 ��y����y2��0
��y����y2��0��
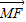 =��
=��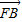 ���ࣨp��-y��=�ˣ�x2-
���ࣨp��-y��=�ˣ�x2-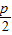 ��y������p=�ˣ�x2-
��y������p=�ˣ�x2-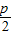 ��
����1������=1����p=�ˣ�x2-
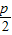 ����y22=2px2��y2��0����x2=
����y22=2px2��y2��0����x2=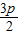 ��y2=
��y2=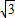 p��
p����B��
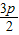 ��
��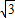 p��
p����ֱ��l��б��k=
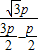 =
=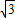 ��
����2��ֱ��l�ķ��̴���y2=2px����ȥy���ɵ�k2x2-��k2p+2p��x+
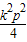 =0����x1x2=
=0����x1x2=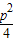
��
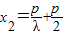 ����
����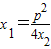 =
=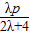
��|
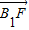 |��|
|��|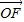 |��2|
|��2|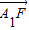 |�ɵȲ�����
|�ɵȲ�������2|
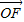 |=|
|=|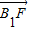 |+2|
|+2|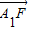 |��
|����
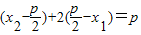
��x2-2x1=
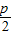
��
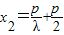 ��
��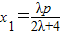 ������ʽ��
������ʽ��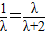 �����=2��
�����=2����3����P��x��x2����S��x1��x12����T��x2��x22�����������x��0��x��±1��x1��x2��
�����P��ԲC2�����߷���Ϊy-x2=k��x-x������y=kx-kx+x2����
��
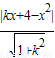 =1��
=1������x2-1��k2+2x��4-x2��k+��x2-4��2-1=0��
��PS��PT��б��Ϊk1��k2��k1��k2������k1��k2���������̵�����������
k1+k2=
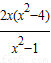 ��k1k2=
��k1k2=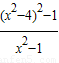 ��
�����ٴ���y=x2����x2-kx+kx-x2=0��
����x�Ǵ˷��̵ĸ�����x1=k1-x��x2=k2-x��
����
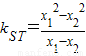 =x1+x2=k1+k2-2x=
=x1+x2=k1+k2-2x=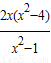 -2x��kNP=
-2x��kNP=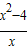 ��
����MP��AB����kNP•kST=[
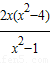 -2x]•
-2x]•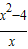 =-1�����x2=
=-1�����x2=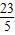 ��
������P��������
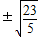 ��
��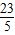 ��������ֱ��l�ķ���Ϊ
��������ֱ��l�ķ���Ϊ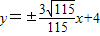 ��
�����������⿼��ֱ���������ߵ�λ�ù�ϵ������Ȳ����е����ʣ�����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ��������
�������� �����й�ͬ���㣬�����ߵĶ���Ϊ��
�����й�ͬ���㣬�����ߵĶ���Ϊ��