题目内容
已知直线l与x轴正方向、y轴正方向交于A,B两点,M,N是线段AB的三等分点,椭圆C经过M,N两点.(1)若直线l的方程为2x+y-6=0,求椭圆C的标准方程;
(2)若椭圆的中心在原点,对称轴在坐标轴上,其离心率e∈(0,
 ),求直线l的斜率k的取值范围.
),求直线l的斜率k的取值范围.
【答案】分析:(1)因为M,N是线段AB的三等分点在坐标轴上,由椭圆标准方程列式求得a、b的值,进而求得椭圆方程;
(2)先设A(m,0),B(0,n),(m>0,n>0),根据分点坐标公式求出M,N的坐标,再就椭圆的焦点在x轴和y轴上分类讨论,结合设而不求的方法即可求出直线l的斜率k的取值范围.
解答:解:(1)依题意A(3,0),B(0,6),
∵M、N是线段AB的三等分点,∴不妨记M(1,4),N(2,2)…(3分)
设椭圆方程为ax2+by2=1(a>0,b>0,a≠b),
则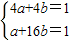 ,解得
,解得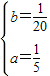 ,…(6分)
,…(6分)
∴椭圆方程为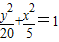 . …(7分)
. …(7分)
(2)设A(m,0),B(0,n),(m>0,n>0),则M(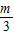 ,
,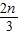 ),N(
),N(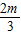 ,
,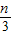 ),
),
…(8分)
①当焦点在x轴上时,设椭圆方程为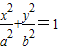 (a>b>0),
(a>b>0),
则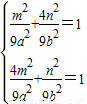 ,
,
∴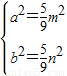 ,得
,得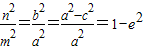 ,…(11分)
,…(11分)
又∵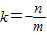 ,
,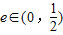 ,
,
∴k∈(-1,-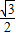 ); …(13分)
); …(13分)
②当焦点在y轴上时,同法可得k∈(-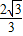 ,-1),
,-1),
综上k∈(-1,-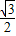 )∪(-
)∪(-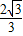 ,-1). …(16分)
,-1). …(16分)
点评:本题考查了椭圆标准方程的定义和求法,椭圆的几何意义,及直线与椭圆的关系,方程思想和分类讨论思想,设而不求解决问题,属基础题.
(2)先设A(m,0),B(0,n),(m>0,n>0),根据分点坐标公式求出M,N的坐标,再就椭圆的焦点在x轴和y轴上分类讨论,结合设而不求的方法即可求出直线l的斜率k的取值范围.
解答:解:(1)依题意A(3,0),B(0,6),
∵M、N是线段AB的三等分点,∴不妨记M(1,4),N(2,2)…(3分)
设椭圆方程为ax2+by2=1(a>0,b>0,a≠b),
则
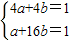 ,解得
,解得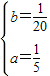 ,…(6分)
,…(6分)∴椭圆方程为
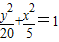 . …(7分)
. …(7分)(2)设A(m,0),B(0,n),(m>0,n>0),则M(
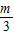 ,
,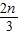 ),N(
),N(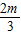 ,
,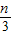 ),
),…(8分)
①当焦点在x轴上时,设椭圆方程为
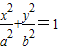 (a>b>0),
(a>b>0),则
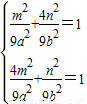 ,
,∴
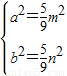 ,得
,得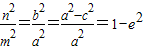 ,…(11分)
,…(11分)又∵
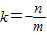 ,
,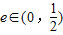 ,
,∴k∈(-1,-
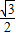 ); …(13分)
); …(13分)②当焦点在y轴上时,同法可得k∈(-
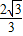 ,-1),
,-1),综上k∈(-1,-
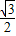 )∪(-
)∪(-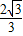 ,-1). …(16分)
,-1). …(16分)点评:本题考查了椭圆标准方程的定义和求法,椭圆的几何意义,及直线与椭圆的关系,方程思想和分类讨论思想,设而不求解决问题,属基础题.

练习册系列答案
相关题目