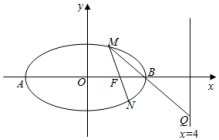
题目内容
【题目】已知离心率为![]() 的椭圆
的椭圆![]()
![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)荐椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,请问
的斜率成等差数列,请问![]() 的面积
的面积![]() 是否为定值?若是,求出此定值;若不是,请说明理由.
是否为定值?若是,求出此定值;若不是,请说明理由.
【答案】(1)![]() ;(2)是,
;(2)是,![]()
【解析】
(1)根据![]() 及
及![]() 可得
可得![]() ,再将点
,再将点![]() 代入椭圆的方程与
代入椭圆的方程与![]() 联立解出
联立解出![]() ,即可求出椭圆的方程;
,即可求出椭圆的方程;
(2) 可设![]() 所在直线的方程为
所在直线的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,用根与系数的关系求出
的方程与椭圆的方程联立,用根与系数的关系求出![]() ,然后将直线
,然后将直线![]() 、
、![]() 、
、![]() 的斜率
的斜率![]() 、
、![]() 、
、![]() 分别用
分别用![]() 表示,利用
表示,利用![]() 可求出
可求出![]() ,从而可确定点
,从而可确定点![]() 恒在一条直线
恒在一条直线![]() 上,结合图形即可求出
上,结合图形即可求出![]() 的面积
的面积![]() .
.
(1)因为椭圆的离心率为![]() ,所以
,所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,①
,①
因为点![]() 在椭圆上,所以
在椭圆上,所以![]() ,②
,②
由①②解得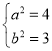 ,所以椭圆C的方程为
,所以椭圆C的方程为![]() .
.
(1)可知![]() ,
,![]() ,可设
,可设![]() 所在直线的方程为
所在直线的方程为![]() ,
,
由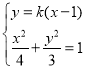 ,得
,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设直线![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() ,
,
因为![]() 三点共线,所以
三点共线,所以![]() ,即
,即![]() ,
,
所以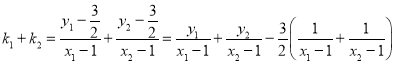
![]() ,
,
又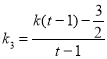 ,
,
因为直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,所以
的斜率成等差数列,所以![]() ,
,
即![]() ,化简得
,化简得![]() ,即点
,即点![]() 恒在一条直线
恒在一条直线![]() 上,
上,
又因为直线![]() 方程为
方程为![]() ,且
,且![]() ,
,
所以![]() 是定值
是定值![]() .
.

【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
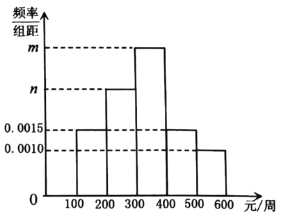
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()