题目内容
设椭圆 的左、右焦点分别为
的左、右焦点分别为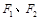 ,上顶点为
,上顶点为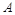 ,离心率为
,离心率为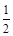 ,在
,在 轴负半轴上有一点
轴负半轴上有一点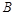 ,且
,且
(1)若过 三点的圆恰好与直线
三点的圆恰好与直线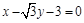 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点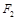 作斜率为
作斜率为 的直线
的直线 与椭圆C交于
与椭圆C交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点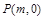 ,使得以
,使得以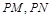 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.

【答案】
1)由题意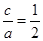 ,得
,得
 ,所以
,所以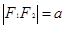
又 由于
由于 ,所以
,所以 为
为 的中点,
的中点,
所以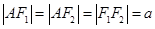
所以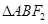 的外接圆圆心为
的外接圆圆心为 ,半径
,半径 …………………3分
…………………3分
又过 三点的圆与直线
三点的圆与直线 相切,
相切,
所以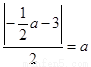 解得
解得 ,
,
所求椭圆方程为 …………………………………………………… 6分
…………………………………………………… 6分
(2)有(1)知 ,设
,设 的方程为:
的方程为: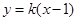
将直线方程与椭圆方程联立
 ,整理得
,整理得
设交点为 ,因为
,因为
则 ……………………………………8分
……………………………………8分
若存在点 ,使得以
,使得以 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以
又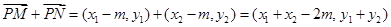
又 的方向向量是
的方向向量是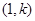 ,故
,故 ,则
,则
 ,即
,即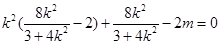
由已知条件知
 ………………………11分
………………………11分
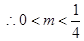 ,故存在满足题意的点
,故存在满足题意的点 且
且 的取值范围是
的取值范围是
【解析】略

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
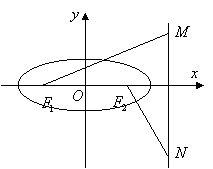
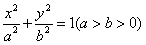 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率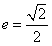 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且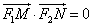 ,
,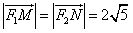 ,求a、b的值;
,求a、b的值;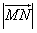 最小时,求证
最小时,求证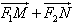 与
与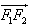 共线。
共线。 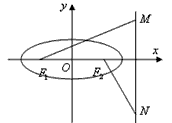
 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.