题目内容
已知向量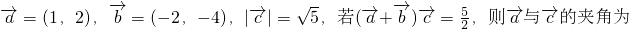
- A.30°
- B.60°
- C.120°
- D.150°
C
分析:先设 与
与 的夹角为θ,根据题意,易得
的夹角为θ,根据题意,易得 =-2
=-2 ,将其代入(
,将其代入( +
+ )=
)= 中易得
中易得 •
• =-
=- ,进而由数量积的运算,可得cosθ的值,有θ的范围,可得答案.
,进而由数量积的运算,可得cosθ的值,有θ的范围,可得答案.
解答:设 与
与 的夹角为θ,
的夹角为θ,
∵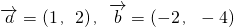 ,则
,则 =-2
=-2 ,
,
( +
+ )•
)• =-
=- •
• =
= ,
,
即 •
• =-
=- ,
,
cosθ=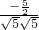 =-
=- ,
,
0°≤θ≤180°,
则θ=120°,
故选C.
点评:本题考查向量的数量积的运用,要求学生能熟练计算数量积并通过数量积来求出向量的模和夹角或证明垂直.
分析:先设
 与
与 的夹角为θ,根据题意,易得
的夹角为θ,根据题意,易得 =-2
=-2 ,将其代入(
,将其代入( +
+ )=
)= 中易得
中易得 •
• =-
=- ,进而由数量积的运算,可得cosθ的值,有θ的范围,可得答案.
,进而由数量积的运算,可得cosθ的值,有θ的范围,可得答案.解答:设
 与
与 的夹角为θ,
的夹角为θ,∵
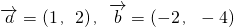 ,则
,则 =-2
=-2 ,
,(
 +
+ )•
)• =-
=- •
• =
= ,
,即
 •
• =-
=- ,
,cosθ=
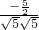 =-
=- ,
,0°≤θ≤180°,
则θ=120°,
故选C.
点评:本题考查向量的数量积的运用,要求学生能熟练计算数量积并通过数量积来求出向量的模和夹角或证明垂直.

练习册系列答案
相关题目
已知向量a、b,若|a|=1,|b|=2,a⊥(a+b ),则a与b夹角的大小为( )
| A、120° | B、90° | C、60° | D、30° |
已知向量
,
,
满足|
|=1,|
|=2,
=
+
,
⊥
,则
与
的夹角等于( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| A、120° | B、60° |
| C、30° | D、90° |
已知向量a,b满足|a|=2,|b|=3,|2a+b|=
,则a与b的夹角为( )
| 37 |
| A、30° | B、45° |
| C、60° | D、90° |