题目内容
【题目】已知函数f(x)= ![]() 设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
设方程f(x)=2﹣x+b(b∈R)的四个实根从小到大依次为x1 , x2 , x3 , x4 , 对于满足条件的任意一组实根,下列判断中一定成立的是( )
A.x1+x2=2
B.e2<x3x4<(2e﹣1)2
C.0<(2e﹣x3)(2e﹣x4)<1
D.1<x1x2<e2
【答案】B
【解析】解:方程f(x)=2﹣x+b(b∈R)的根可化为
函数y=f(x)﹣2﹣x与y=b图象的交点的横坐标,
作函数y=f(x)﹣2﹣x的图象,
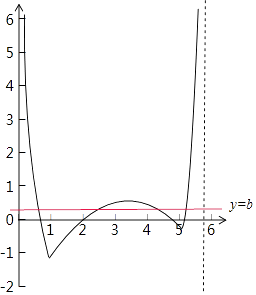
由图象可得,0<x1<1<x2<e<x3<2e﹣1<x4<2e,
故x3x4>e2;
易知|ln(2e﹣x3)|>|ln(2e﹣x4)|,
即ln(2e﹣x3)>﹣ln(2e﹣x4),
即ln(2e﹣x3)+ln(2e﹣x4)>0,
即4e2﹣2e(x3+x4)+x3x4>1,
即2e(x3+x4)<x3x4+4e2﹣1,
∴x3x4<(2e﹣1)2,∴ ![]() ,
,
所以答案是:B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目