题目内容
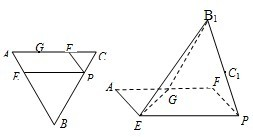 (2013•临沂三模)如图,在边长为3的正三角形ABC中,G、F为边AC的三等分点,E、P分别是AB、BC边上的点,满足AE=CP=1,今将△BEP,△CFP分别沿EP,FP向上折起,使边BP与边CP所在的直线重合,B,C折后的对应点分别记为B1,C1.
(2013•临沂三模)如图,在边长为3的正三角形ABC中,G、F为边AC的三等分点,E、P分别是AB、BC边上的点,满足AE=CP=1,今将△BEP,△CFP分别沿EP,FP向上折起,使边BP与边CP所在的直线重合,B,C折后的对应点分别记为B1,C1.(Ⅰ)求证:C1F∥平面B1GE;
(Ⅱ)求证:PF⊥平面B1EF.
分析:(Ⅰ)取EP的中点D,连接FD、C1D、C1F.利用平行线的性质,证出△B1EP中EP∥GF且EP=GF,从而得到四边形GEDF为平行四边形,得FD∥GE.结合DC1∥EB1且DC1、FD是平面DFC1内的相交直线,GE、B1E是平面B1GE内的相交直线,得到平面DFC1∥平面B1GE,从而证出C1F∥平面B1GE.
(II)连接EF,B1F,由△BEP内由余弦定理算出EF2=3,可得FP2+EF2=EP2,得PF⊥EF.根据△PB1F的中线C1F=
PB1,证出B1F⊥PF,结合线面垂直的判定定理,即可证出PF⊥平面B1EF.
(II)连接EF,B1F,由△BEP内由余弦定理算出EF2=3,可得FP2+EF2=EP2,得PF⊥EF.根据△PB1F的中线C1F=
| 1 |
| 2 |
解答:解:(Ⅰ)取EP的中点D,连接FD、C1D、C1F.
∵BC=3,CP=1,∴折起后C1为B1P的中点.
∴在△B1EP中,DC1∥EB1,…(1分)
又∵AB=BC=AC=3,AE=CP=1,
∴
=
,∴EP=2且EP∥GF.…(2分)
∵G,F为AC的三等分点,∴GF=1.
又∵ED=
EP=1,∴GF=ED,…(3分)
∴四边形GEDF为平行四边形.
∴FD∥GE.…(4分)
又∵DC1∩FD=D,GE∩B1E=E,
∴平面DFC1∥平面B1GE.…(5分)
又∵C1F?平面DFC1
∴C1F∥平面B1GE.…(6分)
(Ⅱ)连接EF,B1F,由已知得∠EPF=60°,且FP=1,EP=2,
由余弦定理,得EF2=12+22-2×1×2×cos60°=3
∴FP2+EF2=EP2,可得PF⊥EF.…(8分)
∵B1C1=PC1=1,C1F=1,得FC1=B1C1=PC1,
∴△PB1F的中线C1F=
PB1,可得△PB1F是直角三角形,即B1F⊥PF.…(10分)
∵EF∩B1F=F,EF、B1F?平面B1EF
∴PF⊥平面B1EF.…(12分)

∵BC=3,CP=1,∴折起后C1为B1P的中点.
∴在△B1EP中,DC1∥EB1,…(1分)
又∵AB=BC=AC=3,AE=CP=1,
∴
| EP |
| AC |
| EB |
| AB |
∵G,F为AC的三等分点,∴GF=1.
又∵ED=
| 1 |
| 2 |
∴四边形GEDF为平行四边形.
∴FD∥GE.…(4分)
又∵DC1∩FD=D,GE∩B1E=E,
∴平面DFC1∥平面B1GE.…(5分)
又∵C1F?平面DFC1
∴C1F∥平面B1GE.…(6分)
(Ⅱ)连接EF,B1F,由已知得∠EPF=60°,且FP=1,EP=2,
由余弦定理,得EF2=12+22-2×1×2×cos60°=3
∴FP2+EF2=EP2,可得PF⊥EF.…(8分)
∵B1C1=PC1=1,C1F=1,得FC1=B1C1=PC1,
∴△PB1F的中线C1F=
| 1 |
| 2 |
∵EF∩B1F=F,EF、B1F?平面B1EF
∴PF⊥平面B1EF.…(12分)
点评:本题以折叠问题为载体,利用面面平行证明线面平行,并证明线面垂直.着重考查了三角形中位线定理、直角三角形的判定、空间线面平行和线面垂直的判定定理等知识,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,
(2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示, (2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( )
(2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( ) (2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )
(2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )