题目内容
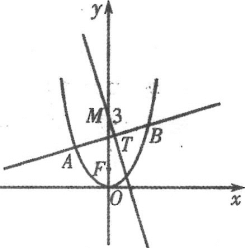
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
【答案】C
【解析】
根据线线平行判定定理、异面直线所成角、直线与平面所成角等知识对选项A、B、C、D进行逐一判断其正确与否.
解:选项A:因为E、F是AD、BD中点,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以EF∥平面![]() ,
,
所以选项A正确;
选项B:因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
且∠BDC=90°,即![]() ,
,
又因为![]() 平面BCD,
平面BCD,
故![]() 平面
平面![]() ,
,
故![]()
![]() ,
,
所以异面直线CD与![]() 所成的角为90°,
所成的角为90°,
选项B正确;
选项C:由选项B可知![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,
因为AD=CD=2,
即![]() =CD=2,
=CD=2,
所以由勾股定理得,![]() ,
,
在![]() 中,
中,
BC=![]() ,
,
在![]() 中,
中,
![]() ,
,
故![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,
,
故选项C错误;
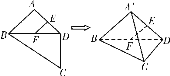
选项D:连接![]()
因为![]()
所以![]()
因为![]() 是中点,
是中点,
所以![]() ,
,
因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
又因为![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面BCD所成的角,
与平面BCD所成的角,
在![]() 中,
中,![]() ,
,![]() ,
,
所以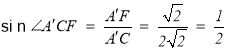 ,
,
所以![]() ,
,
故直线![]() 与平面BCD所成的角为30°,
与平面BCD所成的角为30°,
故选项D正确,
本题不正确的选项为C,故选C.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
【题目】重庆市第八中学校为了解学生喜爱运动是否与性别有关,从全校学生中随机抽取50名学生进行问卷调查,得到如图所示的![]() 列联表.
列联表.
喜爱运动 | 不喜爱运动 | 合计 | |
男生 | 22 | 8 | 30 |
女生 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
附: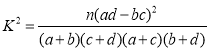 ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)能否有97.5%以上的把握认为“喜爱运动”与“性别”有关;
(2)用分层抽样的方法从被调查的20名女生中抽取5名进行问卷调查,求抽取喜爱运动的女生、不喜爱运动的女生各有多少的人;
(3)在(2)抽取的女生中,随机选出2人进行座谈,求至少有1名是喜爱运动的女生的概率.