题目内容
已知A，B是单位圆（O为圆心）上的两个定点，且∠AOB=60°，若C为该圆上的动点，且
，则xy的最大值为
- A.1
- B.2
- C.
- D.
D
分析：由
，且向量的模都是 1，
•
=0，平方可得1=x2+y2+xy≥3xy，再由x，y∈[0，1]，
可得xy的范围．
解答：由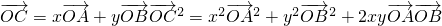
，
又，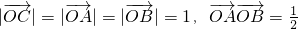
∴1=x2+y2+xy≥3xy，得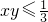
，
而点C在以O为圆心的圆弧
上变动，得x，y∈[0，1]，
于是，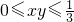
，
故选D．
点评：此题是中档题．本题考查两个向量的数量积的定义以及基本不等式的应用，体现了数形结合的数学思想．
分析：由
，且向量的模都是 1，•=0，平方可得1=x2+y2+xy≥3xy，再由x，y∈[0，1]，可得xy的范围．
解答：由
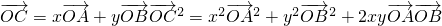，又，
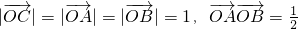
∴1=x2+y2+xy≥3xy，得
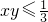，而点C在以O为圆心的圆弧
上变动，得x，y∈[0，1]，于是，
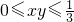，故选D．
点评：此题是中档题．本题考查两个向量的数量积的定义以及基本不等式的应用，体现了数形结合的数学思想．
练习册系列答案
相关题目
如图，已知A、B是单位圆O上的点，C是圆与x轴正半轴的交点，点A的坐标为已知A，B是单位圆上的动点，且|AB|=
，单位圆的圆心为O，则
?
=（ ）
| 3 |
| OA |
| AB |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
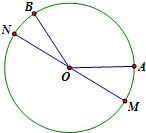已知A，B是单位圆上的两点，O为圆心，且∠AOB=120°，MN是圆O的一条直径，点C在圆内，且满足