题目内容
已知A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与x轴正半轴的交点,△AOB为等腰直角三角形,记∠AOC=α.
(1)求A点的坐标为(
,
),求
的值;
(2)求|BC|的取值范围.
(1)求A点的坐标为(
| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+sin2α |
| cos2α+cos2α |
(2)求|BC|的取值范围.
分析:(1)由A的坐标求出tanα的值,然后把所求式子的分子第二项利用二倍角的正弦函数公式化简,分母第二项利用二倍角的余弦函数公式化简,然后分子分母同时除以cos2α,利用同角三角函数间的基本关系化为关于tanα的式子,把tanα的值代入即可求出值;
(2)由A和B都为单位圆上的点,且C为单位圆与x轴的交点,根据∠AOC=α,且三角形AOB为等腰直角三角形,分别表示出A,B及C的坐标,利用两点间的距离公式表示出|BC|,利用诱导公式及同角三角函数间的基本关系把被开方数化简后,根据A为第一象限的点得出α的范围,进而得出sinα的范围,即可得出|BC|的范围.
(2)由A和B都为单位圆上的点,且C为单位圆与x轴的交点,根据∠AOC=α,且三角形AOB为等腰直角三角形,分别表示出A,B及C的坐标,利用两点间的距离公式表示出|BC|,利用诱导公式及同角三角函数间的基本关系把被开方数化简后,根据A为第一象限的点得出α的范围,进而得出sinα的范围,即可得出|BC|的范围.
解答:解:(1)由已知可得:tanα=
=
=
,(2分)
则
=
(4分)
=
(6分)
=
=20;
(2)根据题意得:A=(cosα,sinα),B=(cos(α+
),sin(α+
)),且C(1,0),
∴|BC|=
=
,(8分)
∵A,B分别在第一、第二象限,且α∈(0,
),
∴sinα∈(0,1),
∴|BC|的范围是(
,2).(12分)
| y |
| x |
| ||
|
| 4 |
| 3 |
则
| sin2α+sin2α |
| cos2α+cos2α |
| sin2α+2sinαcosα |
| cos2α +cos2α-sin2α |
=
| tan2α+2tanα |
| 2-tan2α |
=
(
| ||||
2-(
|
(2)根据题意得:A=(cosα,sinα),B=(cos(α+
| π |
| 2 |
| π |
| 2 |
∴|BC|=
[cos(α+
|
| 2+2sinα |
∵A,B分别在第一、第二象限,且α∈(0,
| π |
| 2 |
∴sinα∈(0,1),
∴|BC|的范围是(
| 2 |
点评:此题考查了三角函数的化简求值,以及正弦函数的值域,涉及的知识有三角函数的定义,二倍角的正弦、余弦函数公式,诱导公式,以及同角三角函数间的基本关系,根据题意表示出三点的坐标是解第二小问的关键.

练习册系列答案
相关题目
 如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为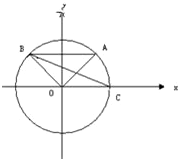
 如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为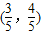 ,点B在第二象限,且△AOB为正三角形.
,点B在第二象限,且△AOB为正三角形.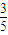 ,
,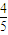 ),求
),求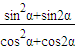 的值;
的值;