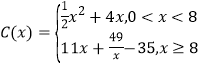题目内容
【题目】设![]() 函数
函数![]() 为
为![]() 的导函数
的导函数
(1)若曲线![]() 与曲线
与曲线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)设函数![]() 若
若![]() 为函数
为函数![]() 的极大值,且
的极大值,且![]()
①求![]() 的值;
的值;
②求证:对于![]() .
.
【答案】(1)![]() .(2)①k=1,②见证明
.(2)①k=1,②见证明
【解析】
(1)由题得![]() 曲线
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,得
,得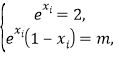 解方程求出m的值.(2) ①,利用导数求出
解方程求出m的值.(2) ①,利用导数求出![]() ,易得函数
,易得函数![]() 在区间
在区间![]() 是减函数,根据单调性求出k的值. ②利用导数求得
是减函数,根据单调性求出k的值. ②利用导数求得![]() ,再证明
,再证明![]() .
.
(1) ![]() ,
,
设切点为![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,
,
结合题设得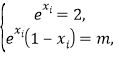
所以![]()
所以实数![]() 的值为
的值为![]() .
.
(2)①:![]() ,
,
所以![]() ,
,
![]() ,
,
![]() 由
由![]() ,得
,得![]() ,
,
即![]() 两根为
两根为![]() ,
,
![]() ,
,
![]() ,因此,
,因此,
|
|
|
|
|
|
|
| 0 | + | 0 |
|
|
| 极小值 |
| 极大值 |
|
结合题设,有![]()
![]() ,
,
易知函数![]() 在区间
在区间![]() 是减函数,
是减函数,
因此,![]() 时,
时,![]() ,即
,即![]()
![]() .
.
②证明:由由①,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 在
在![]() 是减函数,
是减函数,
所以![]() 时,
时,![]() ,
,
由①,![]() 时,
时,![]() ,
,
所以![]() ,
,![]() ,
,
即对于![]() 成立.
成立.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目