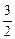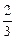题目内容
求证:任何一个实系数一元三次方程a0x3+a1x2+a2x+a3=0(a0,a1,a2,a3∈R,a0≠0)至少有一个实数根.
证明略
设f(x)=a0x3+a1x2+a2x+a3,函数f(x)在(-∞,+∞)连续,
且x→+∞时,f(x)→+∞;x→-∞时,f(x)→-∞,
所以必存在a∈(-∞,+∞),b∈(-∞,+∞),使f(a)·f(b)<0,
所以f(x)的图像至少在(a,b)上穿过x轴一次,即f(x)=0至少有一实根.
且x→+∞时,f(x)→+∞;x→-∞时,f(x)→-∞,
所以必存在a∈(-∞,+∞),b∈(-∞,+∞),使f(a)·f(b)<0,
所以f(x)的图像至少在(a,b)上穿过x轴一次,即f(x)=0至少有一实根.

练习册系列答案
相关题目
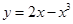 在横坐标为
在横坐标为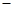 l的点处的切线为
l的点处的切线为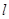 ,则点P(3,2)到直线
,则点P(3,2)到直线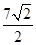
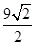
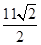
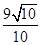
 ,则函数
,则函数 点P(1,
点P(1, )的切线与两坐标轴围成的三角形的面积为 。
)的切线与两坐标轴围成的三角形的面积为 。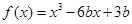 在(0,1)内有极小值,则实数b的取值范围是( )
在(0,1)内有极小值,则实数b的取值范围是( )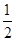 )
)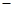 ∞,1)
∞,1)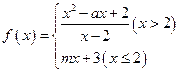 在点
在点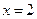 处连续,则
处连续,则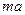 的值是 .
的值是 . 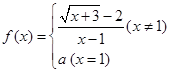 在
在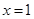 处连续,则
处连续,则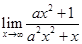 =( )
=( )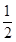
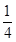
 成等差,且
成等差,且 成等比。则
成等比。则 值为
值为 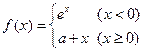 为R上的连续函数,则( )
为R上的连续函数,则( )



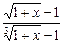 在点x=0处连续,则f(0)等于( )
在点x=0处连续,则f(0)等于( )