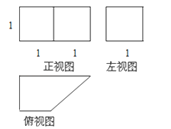
题目内容
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,(
,( ![]() ),设
),设![]()
(1)若![]() ,求证:
,求证: ![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若![]() ,又数列
,又数列![]() 满足:
满足: ![]() :
:
①求数列![]() 的前
的前![]() 和
和![]() ;
;
②求证:数列![]() 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:
(1)由![]() ,得故
,得故![]() ,进而
,进而![]() ,可得数列
,可得数列![]() 为等比数列,即可求解数列的通项公式;
为等比数列,即可求解数列的通项公式;
(2)①由(1)得![]() ,利用乘公比错位相减法,即可求解数列的前
,利用乘公比错位相减法,即可求解数列的前![]() 项和.
项和.
②证明:由(1)得![]() ,对于给定的
,对于给定的![]() ,若存在
,若存在![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
,
得出取![]() ,则
,则![]() ,使得
,使得![]() ,得以证明.
,得以证明.
试题解析:
(1)因为![]() .
.
故![]() ,即
,即![]() ,所以
,所以![]()
故数列![]() 为等比数列,且
为等比数列,且![]() ,所以
,所以![]()
(2)![]()
![]()
![]() ,故数列
,故数列![]() 是以
是以![]() 为首项,
为首项, ![]() 为公差的等差数列,
为公差的等差数列,
易求出![]()
①![]()
![]() ,
, ![]()
![]()
以上两式相减得: ![]()
![]()
![]()
所以![]()
②证明:由![]() 且
且![]() ,知
,知![]() ,
,
对于给定的![]() ,若存在
,若存在![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
,
只需![]() ,只需
,只需![]()
取![]() ,则
,则![]()
所以对于数列![]() 中的任意一项
中的任意一项![]() ,
,
都存在![]() 与
与![]() ,使得
,使得![]() ,
,
即数列![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.

【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中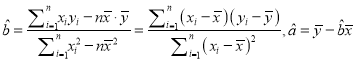 .
.
【题目】小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5---10 | 6.5---8.5 |
某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是:未来一年内,位于一类风区的A项目获利![]() %的可能性为0.6,亏损
%的可能性为0.6,亏损![]() %的可能性为0.4;
%的可能性为0.4;
B项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2.
假设投资A项目的资金为![]() (
(![]() )万元,投资B项目资金为
)万元,投资B项目资金为![]() (
(![]() )万元,且公司要求对A项目的投资不得低于B项目.
)万元,且公司要求对A项目的投资不得低于B项目.
(Ⅰ)记投资A,B项目的利润分别为![]() 和
和![]() ,试写出随机变量
,试写出随机变量![]() 与
与![]() 的分布列和期望
的分布列和期望![]() ,
, ![]() ;
;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和![]() 的最大值,并据此给出公司分配投资金额建议.
的最大值,并据此给出公司分配投资金额建议.