题目内容
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=![]() ,BD=CD=1,另一个侧面是正三角形.
,BD=CD=1,另一个侧面是正三角形.
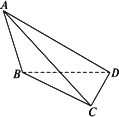
(1)求证:AD⊥BC.
(2)求二面角B-AC-D的大小.
(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由.
答案:
解析:
提示:
解析:
|
解:(1)方法一:如图所示,作AH⊥面BCD于H,连DH.
AB⊥BD ∴AB= ∴AD⊥BC. 方法二:如上图所示,取BC的中点O,连AO、DO. 则有AO⊥BC,DO⊥BC,∴BC⊥面AOD. ∴BC⊥AD. (2)BM⊥AC于M,作MN⊥AC交AD于N,则∠BMN就是二面角B-AC-D的平面角,因为AB=AC=BC= ∴∠BMN=arccos (3)设E是所求的点,作EF⊥CH于F,连FD.则EF∥AH,∴EF⊥面BCD,∠EDF就是ED与面BCD所成的角,则∠EDF=30°.设EF=x,易得AH=HC=1,则CF=x,FD= 故线段AC上存在E点,且CE=1时,ED与面BCD成30°角. |
提示:
|
线线垂直 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
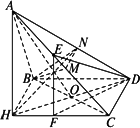
 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC, 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=