题目内容
(本小题12分)已知函数 .
.
(1)证明函数 的图像关于点
的图像关于点 对称;
对称;
(2)若 ,求
,求 ;
;
(3)在(2)的条件下,若
 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切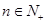 都成立,试求实数
都成立,试求实数 的取值范围.
的取值范围.
【答案】
(1) 证明:见解析;(2) ;(3)
;(3) .
.
【解析】(1)证明f(x)关于点 对称,只须证明:设
对称,只须证明:设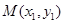 、
、 是函数
是函数 图像上的两点, 其中
图像上的两点, 其中 且
且 ,即证:
,即证: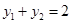 即可.
即可.
(2)利用(1)的结论,采用倒序相加的方法求和即可。
(3)当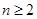 时,
时, , 当
, 当 时,
时, ,
,
 .可求出
.可求出
然后再本小题可转化为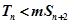 对一切
对一切 都成立,即
都成立,即 恒成立,又即
恒成立,又即
 恒成立,再构造
恒成立,再构造 ,研究其最大值即可。
,研究其最大值即可。
(1)
证明:因为函数 的定义域为
的定义域为 ,
设
,
设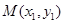 、
、 是函数
是函数 图像上的两点, 其中
图像上的两点, 其中 且
且 ,
,
则有

因此函数图像关于点 对称
……………………………………4分
对称
……………………………………4分
(2)由(1)知当 时,
时,
 ①
①
 ②
②
①+②得 ………………………………………………………………8分
………………………………………………………………8分
(3)当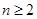 时,
时,
当 时,
时, ,
,

当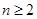 时,
时,  …
… =
= 
∴ (
( )
)
又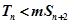 对一切
对一切 都成立,即
都成立,即 恒成立
恒成立
∴ 恒成立,又设
恒成立,又设 ,
,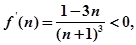 所以
所以 在
在 上递减,所以
上递减,所以 在
在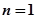 处取得最大值
处取得最大值
∴ ,即
,即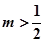
所以 的取值范围是
的取值范围是 ………………12分
………………12分

练习册系列答案
相关题目
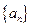 中,
中,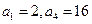 。
。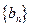 中,
中, ,求数列
,求数列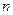 项和
项和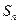 .
.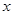 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=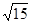 ,求抛物线的方程
,求抛物线的方程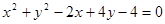 ;
;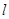 过
过 且与圆C相切,求直线
且与圆C相切,求直线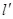 ,使直线
,使直线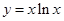
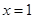 处的切线方程。
处的切线方程。