题目内容
(本小题12分)
已知圆C: ;
;
(1)若直线 过
过 且与圆C相切,求直线
且与圆C相切,求直线 的方程.
的方程.
(2)是否存在斜率为1直线 ,使直线
,使直线 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】
(1)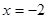 或
或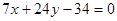
(2)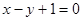 或
或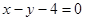
【解析】(1)解:圆C可化为: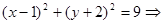 圆心:
圆心: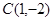 ;半径:
;半径: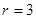
① 当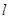 斜率不存在时:
斜率不存在时: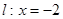 ,满足题意……………………………………(2分)
,满足题意……………………………………(2分)
② 当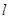 斜率存在时,设斜率为
斜率存在时,设斜率为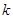 ,则:
,则: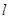 :
: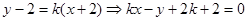
则: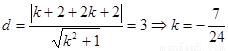
故: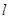 :
: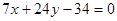 ………………………………………………(3分)
………………………………………………(3分)
综上之:直线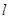 的方程:
的方程: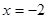 或
或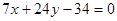 ……………………(1分)
……………………(1分)
(2)解:设直线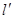 的方程:
的方程: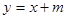
而圆C的圆心: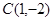 ,则
,则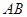 的中垂线方程是:
的中垂线方程是: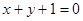
则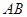 的中点
的中点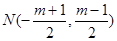 ……………………………………………(2分)
……………………………………………(2分)
而以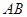 为直径的圆过原点
为直径的圆过原点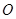 ,则:
,则: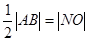
即: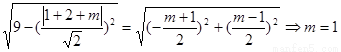 或
或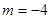 ……(3分)
……(3分)
故所求直线存在,直线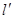 的方程:
的方程: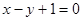 或
或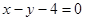 ……………(1分)
……………(1分)

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
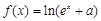 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围; 的方程
的方程 的根的个数.
的根的个数. 满足
满足 且
且 .
. 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 ,求
,求 的最大值;
的最大值;  ,离心率为
,离心率为 ,且过点
,且过点 ,
,
 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。 直线
直线 ,且直线
,且直线 与曲线
与曲线 相切于点
相切于点 ,求直线
,求直线 的坐标。
的坐标。