题目内容
(本小题12分)
已知顶点在原点,焦点在 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程
【答案】
解:设抛物线的方程为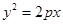 ,则
,则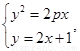 消去
消去 得
得
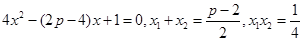
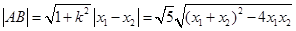
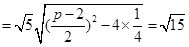 ,
,
则

【解析】略

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
题目内容
(本小题12分)
已知顶点在原点,焦点在 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程
解:设抛物线的方程为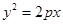 ,则
,则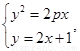 消去
消去 得
得
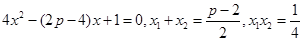
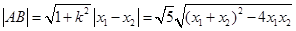
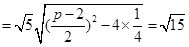 ,
,
则

【解析】略

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案