题目内容
下列说法错误的是( )A.“
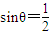 ”是“θ=30°”的充分不必要条件
”是“θ=30°”的充分不必要条件B.命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
C.若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0
D.如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题
【答案】分析:A:由特殊角的三角函数得:“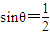 ”是“θ=30°”的必要不充分条件.
”是“θ=30°”的必要不充分条件.
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题.
C:特称命题的否定是全称命题.
D:如果命题“¬p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题.
解答:解:A:由特殊角的三角函数得:若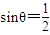 ,则θ不一定为30°;但是若θ=30°,则
,则θ不一定为30°;但是若θ=30°,则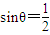 ,所以“
,所以“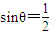 ”是“θ=30°”的必要不充分条件,所以选A.
”是“θ=30°”的必要不充分条件,所以选A.
B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题,所以不选B.
C:根据特称命题的否定是全称命题可得:若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0是正确的,所以C不能选.
D:如果命题“¬p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题,所以不选D.
故选A.
点评:本题主要考查必要条件、充分条件、充要条件的判断与复合命题的真假,以及四种命题、特称命题的否命题,此题属于基础题.
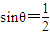 ”是“θ=30°”的必要不充分条件.
”是“θ=30°”的必要不充分条件.B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题.
C:特称命题的否定是全称命题.
D:如果命题“¬p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题.
解答:解:A:由特殊角的三角函数得:若
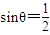 ,则θ不一定为30°;但是若θ=30°,则
,则θ不一定为30°;但是若θ=30°,则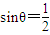 ,所以“
,所以“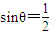 ”是“θ=30°”的必要不充分条件,所以选A.
”是“θ=30°”的必要不充分条件,所以选A.B:根据否命题的概念可得对原命题的条件与结论都进行否定,即可得到原命题的否命题,所以不选B.
C:根据特称命题的否定是全称命题可得:若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0是正确的,所以C不能选.
D:如果命题“¬p”是真命题,则p是假命题,又因为命题“p或q”是真命题,所以q是真命题,所以不选D.
故选A.
点评:本题主要考查必要条件、充分条件、充要条件的判断与复合命题的真假,以及四种命题、特称命题的否命题,此题属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
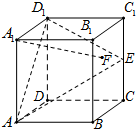 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )| A、点F的轨迹是一条线段 | ||
| B、A1F与D1E不可能平行 | ||
| C、A1F与BE是异面直线 | ||
D、tanθ≤2
|
 如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )