题目内容
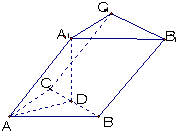 如图,已知三棱柱ABC-A1B1C1的侧棱长与底面边长都等于1,A1在底面ABC上的射影D为BC的中点,则侧棱AA1与底面ABC所成角的大小为
如图,已知三棱柱ABC-A1B1C1的侧棱长与底面边长都等于1,A1在底面ABC上的射影D为BC的中点,则侧棱AA1与底面ABC所成角的大小为分析:由题意可得A1D⊥平面ABC 从而可得∠A1AD即为直线与平面所成的角在Rt△A1AD中cos∠A1AD=
,从而可求;而S△ABC=
×1×
=
,棱柱的高AD=
,代入柱体体积公式可求
| AD |
| AA1 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
解答:解:由题意可得A1D⊥平面ABC∴∠A1AD即为直线与平面所成的角
在Rt△A1AD中,AA1=1,AD=
,A1D=
∴cos∠A1AD=
=
∴∠A1AD=
即直线AA1与平面ABC所成的角为
∵S△ABC=
×1×
=
∴VABC-A1B1C1=
×
=
故答案为:
,
.
在Rt△A1AD中,AA1=1,AD=
| ||
| 2 |
| 1 |
| 2 |
∴cos∠A1AD=
| AD |
| AA1 |
| ||
| 2 |
| π |
| 6 |
即直线AA1与平面ABC所成的角为
| π |
| 6 |
∵S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴VABC-A1B1C1=
| ||
| 4 |
| 1 |
| 2 |
| ||
| 8 |
故答案为:
| π |
| 6 |
| ||
| 8 |
点评:直线与平面所成的角的求解是立体几何中最基本的试题类型,解决的关键是先找出已知平面的垂线,然后找出所要求解的角,进而在直角三角形中进行求解,而柱体体积公式的应用属于基础试题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.