题目内容
已知△ABC的顶点B(-1,-3),AB边上的高CE所在直线的方程为x-3y-1=0,BC边上中线AD所在直线的方程为8x+9y-3=0.求直线AC的方程.
解:∵CE⊥AB,且直线CE的斜率为
∴直线AB的斜率k=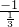 =-3,
=-3,
∴直线AB的方程为y+3=-3(x+1)即3x+y+6=0…(3分)
由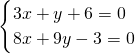 ,解之得
,解之得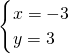 ,
,
∴A点的坐标为(-3,3)…(7分)
设D(a,b),可得C(2a+1,2b+3)
∴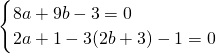 ,解之得
,解之得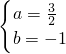
因此D( ,-1),从而可得C(4,1)…(12分)
,-1),从而可得C(4,1)…(12分)
∴直线AC的方程为: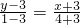 ,
,
化简整理,得2x+7y-15=0,即为直线AC的方程.…(14分)
分析:根据垂直关系算出直线CE的斜率,利用点斜式给出直线AB方程并整理,得AB方程为3x+y+6=0.由AD方程与AB方程联解,可得A(-3,3),结合中点坐标公式解方程组算出C(4,1).最后用直线方程的两点式列式,整理即得直线AC的方程.
点评:本题给出三角形的中线和高所在直线方程,求边AC所在直线的方程.着重考查了直线的基本量与基本形式、直线的位置关系和中点坐标公式等知识,属于基础题.

∴直线AB的斜率k=
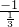 =-3,
=-3,∴直线AB的方程为y+3=-3(x+1)即3x+y+6=0…(3分)
由
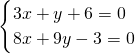 ,解之得
,解之得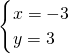 ,
,∴A点的坐标为(-3,3)…(7分)
设D(a,b),可得C(2a+1,2b+3)
∴
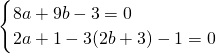 ,解之得
,解之得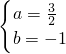
因此D(
 ,-1),从而可得C(4,1)…(12分)
,-1),从而可得C(4,1)…(12分)∴直线AC的方程为:
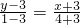 ,
,化简整理,得2x+7y-15=0,即为直线AC的方程.…(14分)
分析:根据垂直关系算出直线CE的斜率,利用点斜式给出直线AB方程并整理,得AB方程为3x+y+6=0.由AD方程与AB方程联解,可得A(-3,3),结合中点坐标公式解方程组算出C(4,1).最后用直线方程的两点式列式,整理即得直线AC的方程.
点评:本题给出三角形的中线和高所在直线方程,求边AC所在直线的方程.着重考查了直线的基本量与基本形式、直线的位置关系和中点坐标公式等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目