题目内容
用反证法证明命题:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那
么a、b、c中至少有一个是偶数时,下列假设中正确的是 ( )
A假设a、b、c都是偶数 B假设a、b、c都不是偶数
C假设a、b、c至多有一个偶数 D假设a、b、c至多有两个偶数
么a、b、c中至少有一个是偶数时,下列假设中正确的是 ( )
A假设a、b、c都是偶数 B假设a、b、c都不是偶数
C假设a、b、c至多有一个偶数 D假设a、b、c至多有两个偶数
B
分析:本题考查反证法的概念,逻辑用语,否命题与命题的否定的概念,逻辑词语的否定.根据反证法的步骤,假设是对原命题结论的否定,故只须对“b、c中至少有一个偶数”写出否定即可.
解答:解:根据反证法的步骤,假设是对原命题结论的否定
“至少有一个”的否定“都不是”.
即假设正确的是:假设a、b、c都不是偶数
故选B.
点评:一些正面词语的否定:“是”的否定:“不是”;“能”的否定:“不能”;“都是”的否定:“不都是”;“至多有一个”的否定:“至少有两个”;“至少有一个”的否定:“一个也没有”;“是至多有n个”的否定:“至少有n+1个”;“任意的”的否定:“某个”;“任意两个”的否定:“某两个”;“所有的”的否定:“某些”.
解答:解:根据反证法的步骤,假设是对原命题结论的否定
“至少有一个”的否定“都不是”.
即假设正确的是:假设a、b、c都不是偶数
故选B.
点评:一些正面词语的否定:“是”的否定:“不是”;“能”的否定:“不能”;“都是”的否定:“不都是”;“至多有一个”的否定:“至少有两个”;“至少有一个”的否定:“一个也没有”;“是至多有n个”的否定:“至少有n+1个”;“任意的”的否定:“某个”;“任意两个”的否定:“某两个”;“所有的”的否定:“某些”.

练习册系列答案
相关题目


 中,得出的一般性结论是 .
中,得出的一般性结论是 .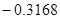 中,用数字
中,用数字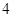 替换其中的一个非
替换其中的一个非 数字后,使所得的数最大,则被替换的数字是:
数字后,使所得的数最大,则被替换的数字是:  照此规律,第
照此规律,第 个等式为________________________________。
个等式为________________________________。
