题目内容
18.设函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),}&{x<1}\\{{2}^{x-1},}&{x≥1}\end{array}\right.$,则f(-2)+f(log212)=( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 先求f(-2)=1+log2(2+2)=1+2=3,再由对数恒等式,求得f(log212)=6,进而得到所求和.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),x<1}\\{{2}^{x-1},x≥1}\end{array}\right.$,
即有f(-2)=1+log2(2+2)=1+2=3,
f(log212)=${2}^{lo{g}_{2}12-1}$=12×$\frac{1}{2}$=6,
则有f(-2)+f(log212)=3+6=9.
故选C.
点评 本题考查分段函数的求值,主要考查对数的运算性质,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
8.已知随机变量X的分布列如下:
(1)求m的值;
(2)求E(X);
(3)若Y=2X-3,求E(Y).
| X | -2 | -1 | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{5}$ | m | $\frac{1}{20}$ |
(2)求E(X);
(3)若Y=2X-3,求E(Y).
3.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,顶角为120°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )


| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$,),k∈z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈z | ||
| C. | (k-$\frac{1}{4}$,k+$\frac{3}{4}$),k∈z | D. | ($2k-\frac{1}{4}$,2k+$\frac{3}{4}$),k∈z |
8.命题“?x0∈(0,+∞),lnx0=x0-1”的否定是( )
| A. | ?x0∈(0,+∞),lnx0≠x0-1 | B. | ?x0∉(0,+∞),lnx0=x0-1 | ||
| C. | ?x∈(0,+∞),lnx≠x-1 | D. | ?x∉(0,+∞),lnx=x-1 |
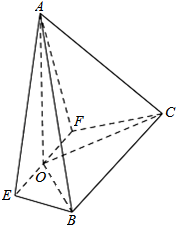 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点. 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.