题目内容
9.${({\sqrt{x}+\frac{2}{x}})^n}$的展开式的二项式系数之和为8,则展开式的常数项等于( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 首先利用二项式系数和得到n,然后利用通项求常数项.
解答 解:因为${({\sqrt{x}+\frac{2}{x}})^n}$的展开式的二项式系数之和为8,所以2n=8,解得n=3,
所以展开式的通项为${C}_{3}^{r}(\sqrt{x})^{3-r}(\frac{2}{x})^{r}={2}^{r}{C}_{3}^{r}{x}^{\frac{3-3r}{2}}$,
所以r=1时,常数项为6;
故选B.
点评 本题考查了二项式的系数以及二项展开式的特征项的求法;关键是求出指数n,利用通项求常数项.

练习册系列答案
相关题目
14.设全集U={1,3,5,7,9},A={1,5,9},B={3,7,9},则(∁UA)∩B=( )
| A. | {3} | B. | {7} | C. | {3,7} | D. | ∅ |
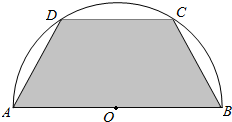 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.