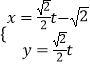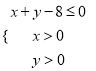题目内容
【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
【答案】
(1)解:当x∈[0,3]时,由于f(x)=2x2﹣3x+1图象的对称轴为 ![]() ,且开口向上,
,且开口向上,
可知 ![]() ,f(x)max=f(3)=10,
,f(x)max=f(3)=10,
所以f(x)的值域 ![]() ;
;
当x∈[0,3]时, ![]() ,
, ![]() ;所以当k>0时,g(x)的值域
;所以当k>0时,g(x)的值域 ![]() ;
;
所以当k<0时,g(x)的值域 ![]() ;
;
又∵AB,所以 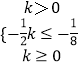 或
或 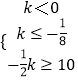 ;
;
即 k≥10或k≤﹣20;
(2)解:∵f(sinx)+sinx﹣a=0,所以2sin2x﹣2sinx+1﹣a=0在x∈[0,2π)上恰有两个解,…
设t=sinx,则t∈[﹣1,1],令h(t)=2t2﹣2t+1﹣a,
①当t∈(﹣1,1)时,由题意h(t)=0恰有一个解或者有两个相等的解,
即h(﹣1)h(﹣1)<0或△=4﹣8(1﹣a)=0,即1<a<5或 ![]()
②若t=﹣1是方程2t2﹣2t+1﹣a=0的一个根,此时a=5,且方程的另一个根为t=2,于是sinx=﹣1或sinx=2,
因此 ![]() ,不符合题意,故a=5(舍);
,不符合题意,故a=5(舍);
③若t=1是方程2t2﹣2t+1﹣a=0的一个根,此时a=1,且方程的另一个根为t=0,于是sinx=1或sinx=0,
因此x=0或 ![]() 或π,不符合题意,故a=1(舍);
或π,不符合题意,故a=1(舍);
综上,a的取值范围是1<a<5或 ![]() .
.
【解析】(1)根据二次函数和正弦函数的图象与性质,分别求出f(x)、g(x)在区间[0,3]上的最值即得值域A、B;再根据AB求出k的取值范围;(2)根据f(sinx)+sinx﹣a=0在x∈[0,2π)上恰有两个解,利用换元法设t=sinx,t∈[﹣1,1],构造函数h(t)=2t2﹣2t+1﹣a,讨论t的取值范围,从而求出实数a的取值范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
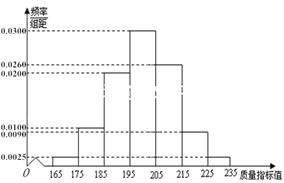
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下:![]() . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过![]() 的概率.
的概率.