题目内容
有3张不透明的卡片，除正面分别写有不同的数字-1、-2、3外，其它均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数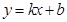
表达式中的
，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数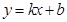表达式中的
则一次函数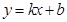的图象经过二、三、四象限的概率是 .
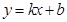表达式中的，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数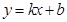表达式中的则一次函数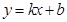的图象经过二、三、四象限的概率是 .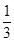
画树状图
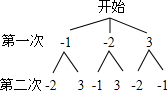
共有6种情况，因为一次函数y=kx+b经过第二、三、四象限，则k＜0，b＜0，又因为k＜0，b＜0的情况有k=-1，b=-2或k=-2，b=-1两种情况，
所以一次函数y=kx+b经过第二、三、四象限的概率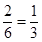为
故答案为：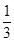
共有6种情况，因为一次函数y=kx+b经过第二、三、四象限，则k＜0，b＜0，又因为k＜0，b＜0的情况有k=-1，b=-2或k=-2，b=-1两种情况，
所以一次函数y=kx+b经过第二、三、四象限的概率为
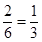故答案为：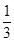
练习册系列答案
相关题目
的方程
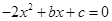，若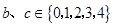
，记“该方程有实数根
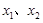且满足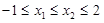
” 为事件A，则事件A发生的概率为（ ）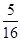
．
，
）
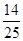
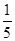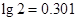