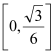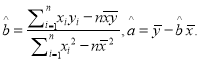题目内容
【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1) ![]() .(2) 2018. (3)当
.(2) 2018. (3)当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.
【解析】试题分析:(1)根据平面向量数量积的坐标表示、二倍角公式和与辅助角公式可得![]() ,根据
,根据![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,确定
,确定![]() ,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)
,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
试题解析:(1) ![]() 向量
向量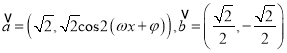 ,
, ![]() ,
, ![]() 点
点![]() 为函数
为函数![]() 图象上的一个最高点,
图象上的一个最高点, ![]() 点
点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,
, ![]() ,
, ![]() 函数
函数![]() 图象过点
图象过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,
, ![]() 的单调增区间是
的单调增区间是![]() .
.
(2) 由(1)知![]() 的周期为
的周期为![]() ,且
,且![]() ,
, ![]() ,而
,而![]() .
.
(3) ![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
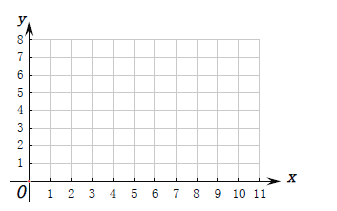
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,
上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,

由图象可知,①当![]() 或
或![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的无公共点,即函数
上的无公共点,即函数![]() 无零点;②当
无零点;②当![]() 与
与![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有一个公共点,即函数
上有一个公共点,即函数![]() 有一个零点;③当
有一个零点;③当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有两个公共点,即函数
上有两个公共点,即函数![]() 有两个零点,综上,当
有两个零点,综上,当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目