题目内容
设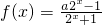 是R上的奇函数.
是R上的奇函数.
(1)求a值;
(2)求f (x)的值域;
(3)若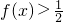 ,求x值范围.
,求x值范围.
解:(1)f (x)是R上的奇函数
∴f(0)=0
∴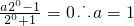
(2)由(1)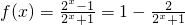
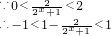
∴f(x)值域为(-1,1)
(3)∵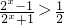 ,
,
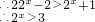
解为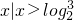
分析:(1)由f (x)是R上的奇函数可得f(0)=0,代入可求a
(2)由(1)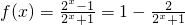 ,结合指数函数的性质可求1+2x的范围,进而可求函数的值域
,结合指数函数的性质可求1+2x的范围,进而可求函数的值域
(3))由题意可得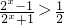 ,整理可求
,整理可求
点评:本题主要考查了奇函数的性质在求解函数解析式中的应用,应用该性质可以简化基本运算,其中指数函数性质的应用是解答本题的关键
∴f(0)=0
∴
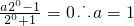
(2)由(1)
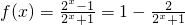
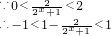
∴f(x)值域为(-1,1)
(3)∵
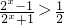 ,
,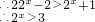
解为
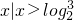
分析:(1)由f (x)是R上的奇函数可得f(0)=0,代入可求a
(2)由(1)
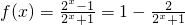 ,结合指数函数的性质可求1+2x的范围,进而可求函数的值域
,结合指数函数的性质可求1+2x的范围,进而可求函数的值域(3))由题意可得
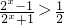 ,整理可求
,整理可求点评:本题主要考查了奇函数的性质在求解函数解析式中的应用,应用该性质可以简化基本运算,其中指数函数性质的应用是解答本题的关键

练习册系列答案
相关题目
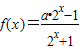 是R上的奇函数.
是R上的奇函数.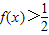 ,求x值范围.
,求x值范围.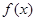 是R上的奇函数,且
是R上的奇函数,且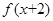 =-
=-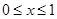 时,
时,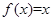 ,则
,则 等于
.
等于
. 是R上的奇函数.
是R上的奇函数.