题目内容
设![]() 是R上的奇函数,且当
是R上的奇函数,且当![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)若![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为
的值域为![]() ,求
,求![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,则
,则![]() ,所以
,所以![]() ,此时
,此时
当![]() 时,
时,![]() ,又
,又![]() ,故
,故
 ………………………………………….4分
………………………………………….4分
(2)解法一:若![]() ,则
,则![]() 在R上单调递增,故
在R上单调递增,故![]() 等价于
等价于
![]() ,令
,令![]() ,
,
于是![]() 在
在![]() 恒成立,…………………2分
恒成立,…………………2分
即![]()
因为![]() 的最大值为
的最大值为![]() ,所以
,所以![]() .…………………3分
.…………………3分
解法二:若![]() ,则
,则![]() 在R上单调递增,故
在R上单调递增,故![]() 等价于
等价于
![]() ,令
,令![]() ,
,
于是![]() 在
在![]() 恒成立,…………………2分
恒成立,…………………2分
设![]()
(1)![]() ,解得:
,解得:![]() ;
;
(2)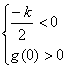 ,解的
,解的![]() .
.
综上,![]() .…………………3分
.…………………3分
(3)首先需满足![]() 在
在![]() 上恒成立,
上恒成立,
于是![]() ,即
,即![]() ;…………………2分
;…………………2分
其次需要![]() 在
在![]() 上的值域为
上的值域为![]() ,即
,即![]() 在
在![]() 上有解
上有解
于是![]() ;
;
综上![]() .
.

练习册系列答案
相关题目
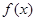 是R上的奇函数,且
是R上的奇函数,且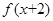 =-
=-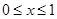 时,
时,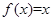 ,则
,则 等于
.
等于
.