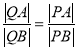题目内容
【题目】如图①,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起,使
折起,使![]() ,连接
,连接![]() 、
、![]() ,得到如图②所示的几何体.
,得到如图②所示的几何体.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在线段
在线段![]() 上,直线
上,直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
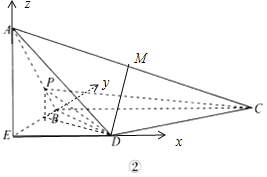
【答案】(1)见解析;(2)![]()
【解析】
(1)取AC中点M,建系,利用向量证明DM⊥AB,DM⊥BC即可得出DM⊥平面ABC,故而平面ACD⊥平面ABC;(2)做出直线PD与平面BCD所成角,求出P到平面BCDE的距离,代入体积公式即可.
(1)证明:∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线为坐标轴建立空间直角坐标系如图:
所在直线为坐标轴建立空间直角坐标系如图:
则![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
设![]() ,则
,则![]() ,故
,故![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .∴
.∴![]() ,
,
∴三棱锥![]() 的体积
的体积![]() .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】某初级中学共有学生2000名,各年级男生女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(1)求x的值.
(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.
【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片.把每列标号最小的卡片选出,将这些卡片中标号最大的数设为a;把每行标号最大的卡片选出,将这些卡片中标号最小的数设为b.
甲同学认为a有可能比b大,乙同学认为a和b有可能相等.那么甲乙两位同学中说法正确的同学是_______.