题目内容
【题目】如图,在![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,
,![]() .
.
(1)求![]() ;
;
(2)若![]() 的面积是
的面积是![]() ,求
,求![]() .
.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)在![]() 中对角
中对角![]() 使用余弦定理求出
使用余弦定理求出![]() 的值,并判断出
的值,并判断出![]() 的形状,从而得出
的形状,从而得出![]() ;
;
(2)解法1:利用![]() 的面积求出
的面积求出![]() ,在该三角形中使用余弦定理求出
,在该三角形中使用余弦定理求出![]() ,利用正弦定理求出
,利用正弦定理求出![]() ,最后利用同角三角函数求出
,最后利用同角三角函数求出![]() ;
;
解法2:作![]() ,垂足为点
,垂足为点![]() ,结合
,结合![]() 的形状可求出
的形状可求出![]() ,由
,由![]() 的面积求出
的面积求出![]() ,并求出
,并求出![]() ,然后利用勾股定理求出
,然后利用勾股定理求出![]() ,然后在
,然后在![]() 中利用锐角三角函数求出
中利用锐角三角函数求出![]() 。
。
(1)在![]() 中,因为
中,因为![]() ,
,![]() ,
,![]()
由余弦定理得![]() ,
,
![]()
整理得![]() ,
,
解得![]() .
.
所以,![]() .
.
所以,![]() 是等边三角形,所以,
是等边三角形,所以,![]() .
.
(2)法1:因为![]() ,所以
,所以![]() .
.
因为![]() 的面积是
的面积是![]() ,
,
所以,![]() ,
,
所以,![]() .
.
在![]() 中,
中,
![]()
![]()
=![]()
所以![]() .
.
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
![]()
易知角![]() 为锐角,
为锐角,
![]()
法2:作![]() ,垂足为
,垂足为![]() ,
,
因为![]() 的等边三角形,
的等边三角形,
所以,![]()
因为![]() 的面积是
的面积是![]() ,
,
所以,![]() ,
,![]()
![]()
在![]() 中,
中,![]()
所以,在![]() 中,
中,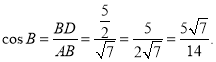

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




